들어가기

모든 데이터 분석의 기초라고 할 수 있는 선형회귀분석은 다음과 같은 모형을 기초로 분석을 합니다.

\[\mathbb{E}[y|x_1, x_2, \cdots, x_p] = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots \beta_p x_p\]

만약 \(\beta_0, \beta_1, \cdots \beta_p\) 가 주어졌다면 설명변수 \(x_1, x_2, \cdots x_p\) 로 결과변수 \(y\) 의 평균을 예측할 수 있습니다.

좀 더 친근한 예를 들어봅시다. 키와 성별을 통해 체중을 예측하고자 할 때, 선형회귀분석은 다음의 모형을 기초로 한다.

\[\mathbb{E}[\textrm{weight}|\textrm{height}, \textrm{gender}] = \beta_0 + \beta_1 \textrm{height} + \beta_2 \textrm{gender}\]

만약 \(\beta_0=-80, \beta_1=0.8, \beta_2=10\) 이라면, 선형회귀식은 \(\mathbb{E}[\textrm{weight}|\textrm{height}, \textrm{gender}] = -80 + 0.8 \times \textrm{height} + 10\times \textrm{gender}\) 이 된다. 만약 키(hegiht)가 180, 성별 남자(gender=1)일 때, 키는 평균 \(\mathbb{E}[\textrm{weight}|\textrm{weight}=180, \textrm{gender}=1]= -80 + 0.8 \times 180 + 10\times 1 = 74\) 로 예측된다. 회귀분석은 자료를 통해 \(\beta_0, \beta_1, \beta_2\) 를 추정하게 된다.

carData 패키지의 Davis에는 남/녀(sex)의 키(height)와 체중(weight) 데이터가 들어 있다. 이에 대해 위의 모형으로 회귀분석을 해본다면 다음과 같다.

library(dplyr)
data(Davis, package='carData')
Davis %>% filter(height > 100) -> Davis2
lm(weight ~ height + sex, data=Davis2)

## 
## Call:
## lm(formula = weight ~ height + sex, data = Davis2)
## 
## Coefficients:
## (Intercept)       height         sexM  
##    -76.6362       0.8107       8.2162

Davis2 %>% mutate(sex = forcats::fct_relevel(sex, "M")) %>% 
  ggplot(aes(x=height, y=weight, col=sex)) + geom_point(alpha=0.7) + 
  #geom_smooth(method='lm')+
  scale_color_discrete_diverging(palette='Blue-Red 3')

결과를 보면 \(\hat{\beta_0}=-76.6362\), \(\hat{\beta_1}=0.8107\), \(\hat{\beta_2}=8.2162\) 이다. \(\hat{}\) 은 자료를 통해 추정된 값임을 나타낸다.

선형회귀 분석의 선형

모형 \(\mathbb{E}[y|x_1, x_2, \cdots, x_p] = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots \beta_p x_p\) 에서 자료를 통해 추정해야하는 \(\beta_0, \beta_1, \cdots, \beta_p\) 를 모수 또는 파라메터(parameter)라고 한다. 선형회귀분석에서 선형은 회귀식이 모수의 선형 함수임을 의미한다.

예를 들어 \(f(x_1) = \beta_0 + \beta_1 x_1 + \beta_2 x_1^2\) 은 \(\beta_0, \beta_1, \beta_2\) 의 선형 함수입니다. 반면 \(f(x_1) = \beta_0 + \beta_1(x_1 + \beta_2 )^2\) 의 경우는 \(\beta_0, \beta_1\cdot\beta_2, \beta\cdot\beta_2^2\) 등을 포함하고 있기 때문에 \(\beta_0, \beta_1, \beta_2\) 의 선형 함수가 아닙니다.

두 함수는 모두 같은 형태( \(x_1\) 의 이차함수)이지만 하나는 계수의 선형 함수[^1]이고, 다른 하나는 그렇지 않다는 점에 주목하길 바랍니다.

[^1]: 선형 모형 \(\mathbb{E}[y | x_1] = \beta_0 + \beta_1 x_1\) 에서 \(\beta_0, \beta_1\) 은 선형모형의 모수라고도 하고, 절편(intercept)과 \(x_1\) 의 계수(coefficient)라고도 합니다.

선형 모형의 장점

선형 모형은 계수의 추정이 다른 모형보다 쉽고 빠르다는 장점이 있습니다.

일반적으로 \(\mathbb{E}[y|x_1, x_2, \cdots, x_p] = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots \beta_p x_p\) 의 계수를 추정하는 식은 다음과 같습니다.

만약 \(i\)-번째 관측값을 \(x_{i1}, x_{i2}, \cdots, x_{ip}, y_i\) 라고 놓으면, 위의 식은 다음과 같이 쓸 수 있습니다.

\[y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots \beta_p x_{ip} + e_i, \ \ e_i \sim \mathcal{N}(0, \sigma^2)\]

\(i\) -번째 관측값과 \(k\) -번째 예측 변수는 \(x_{ik}\) 로 나타내었습니다. 만약 두 변수 \(i\) , \(k\) 가 모두 아랫첨자로 되어 있어 헷갈린다면 \(x_i^{(k)}\) 로 쓸 수도 있습니다. 그렇게 표기하면 위의 식은 다음과 같이 쓸 수 있습니다.

\[y^{(i)} = \beta_0 + \beta_1 x_{1}^{(i)} + \beta_2 x_{2}^{(i)} + \cdots \beta_p x_{p}^{(i)} + e^{(i)}, \ \ e^{(i)} \sim \mathcal{N}(0, \sigma^2)\]

참고로 \(\mathcal{N}(0, \sigma^2)\) 는 오차항 \(e^{(i)}\) 가 모두 평균 \(0\) , 분산 \(\sigma^2\) 의 정규분포를 따르고 있음을 나타냅니다.

위의 식에서 오차항을 제외한 \(y^{(i)}\) 의 추정값은 \(\beta_0 + \beta_1 x_{1}^{(i)} + \beta_2 x_{2}^{(i)} + \cdots \beta_p x_{p}^{(i)}\) 이고, 모든 관찰값에 대해 이 값을 구해서 열벡터로 만들어 본다면 다음과 같습니다.

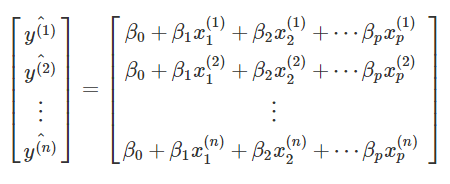
여기서 우변은 행렬의 곱셈으로 다음과 같이 나타낼 수 있습니다.

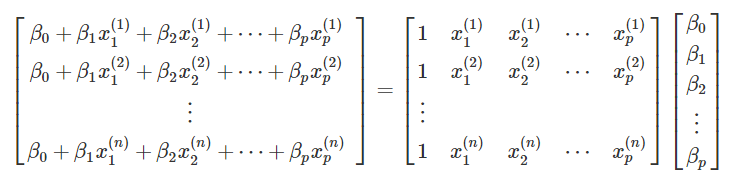
이들을 간단하게 행렬 \(\mathbf{X}\) 와 열 벡터 \(\vec{\beta}\) 로 쓰겠습니다. \(\mathbf{X}\) 는 자료로 주어진 부분(예측 변수)이고, 우리가 추정해야 할 모수(파라메터)는 \(\vec{\beta}\) 입니다.

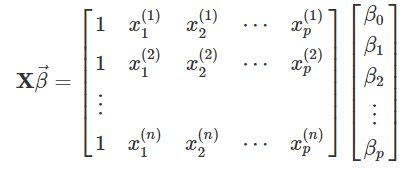
그리고 결과 변수 \(y^{(i)}\) 를 모두 모아 \(\vec{y}\) 으로 나타냅니다.

\(i\) -번째 오차 \(e^{(i)}\) 도 모두 모아 \(\vec{e}\) 로 표기하면 다음이 성립합니다.

\[\vec{e} = \vec{y} – \mathbf{X} \vec{\beta}\]

여기서 오차와 \(\vec{\beta}\) 는 우리가 유한개의 관찰값으로 정확하게 알 수 없는 값입니다.

\(\vec{\beta}\) 를 추정하는 한 가지 방법은 오차들은 오차제곱합(SSE; Sum of Squares Error)을 최소화하는 모수를 구하는 것입니다.

오차제곱합은 다음과 같이 나타낼 수 있습니다.

\[\hat{\vec{e}}^T \hat{\vec{e}} = (\vec{y} – \mathbf{X} \hat{\vec{\beta})}^T (\vec{y} – \mathbf{X} \hat{\vec{\beta})}\]

\((\vec{y} – \mathbf{X} \hat{\vec{\beta})}^T (\vec{y} – \mathbf{X} \hat{\vec{\beta}})\) 에서 \(\vec{y}\) 와 \(\mathbf{X}\) 는 모두 자료에서 주어진 값들로 구성되고, 우리가 모르는 값은 \(\hat{\vec{\beta}}\) 입니다. \(\hat{\vec{\beta}}\) 에 서로 다른 값을 대입함에 따라 오차제곱합의 크기도 다르게 추정되는 데, (추정) 오차제곱합의 크기를 최소로하는 \(\hat{\vec{\beta}}\) 로 \(\vec{\beta}\) 를 추정하는 것이 흔히 말하는 최소제곱법(method of least squares)입니다.

행렬을 활용한 최소제곱법은 다음 시간에 설명하겠습니다. 어쨋든 선형 모형의 장점은 모든 모형을 \(\vec{y} = \mathbf{X} \vec{\beta} + \vec{e}\) 로 나타낼 수 있으며, \(\vec{\beta}\) 를 최소제곱법으로 추정하는 잘 알려진 방법이 존재한다는 것입니다. 그리고 행렬이론을 통해 최소제곱법으로 \(\vec{\beta}\) 을 유일하게 추정할 수 있는 경우와 그렇지 않은 경우 등도 확인할 수도 있습니다.

\(\mathbf{X}\) 를 결정하는 방법

앞에서 봤듯이 선형 모형과 자료가 주어지면 \(\vec{y}\) 와 \(\mathbf{X}\) 가 결정됩니다. 하지만 흔히 모형 행렬(model matrix)로 불리는 \(\mathbf{X}\) 를 결정하는 방법은 여러 가지가 있습니다.

앞에서 들었던 예를 봅시다.

\(f(x_1) = \beta_0 + \beta_1 x_1 + \beta_2 x_1^2\) 과 \(f(x_1) = \beta_0 + \beta_1(x_1 + \beta_2 )^2\) 는 모두 \(x_1\) 의 이차 함수를 나타냅니다.

두 함수를 다시 정리해보면 다음과 같습니다.

\[f(x_1) = \beta_0 + \beta_1 x_1 + \beta_2 x_1^2\]
\[f(x_1) = (\beta_0+\beta_1\beta_2^2) + (2\beta_1 \beta_2) x_1 + \beta_1 x_1^2\]

계수의 선형 함수에서도 동일한 함수를 다른 방법으로 나타낼 수 있습니다. 다음의 예를 봅시다.

\[f(x_1, x_2) = \beta_0 + \beta_1 x_1 + \beta_2 x_2\]
\[f(x_1, x_2) = \beta_0 + \beta_1 x_1 + \beta_2 (x_2-x_1) = \beta_0 + (\beta_1 – \beta_2) x_1 + \beta_2 x_2\]

두 함수 모두 같은 모형을 나타낼 수 있습니다. 예를 들어 \(f(x1, x2) = 1-2 \cdot x_1 + 1\cdot x_2\) 은 \(1-1\cdot x_1 + 1\cdot(x_2-x_1)\) 로도 쓸 수 있습니다.

이 부분은 특히 범주형 변수를 포함하는 선형 모형에서 중요하게 됩니다.

요약/정리

• 여기서는 흔히 말하는 선형 모형(linear model)에서 선형의 의미를 알아보았습니다. 그리고 선형 모형을 행렬식으로 표현해보았습니다. 다음에는 모형 행렬 \(\mathbf{X}\) 를 결정하는 서로 다른 방법들에 대해 알아보고, 실제 선형 모형을 분석하는 R의 명령어(lm; linear model)에서 모형 행렬을 결정하는 방법에 대해 알아보겠습니다.

[참고] 선형 함수

선형 함수란 입력값의 변화량에 출력값의 변화량이 항상 비례하는 함수로 다음과 같은 형식이다. 예를 들어 어떤 함수 \(f(x_1, x_2)\) 가 선형 함수라면 다음을 만족한다.

\[f(x_{11}, x_2)-f(x_{10},x_2) = \alpha_1 (x_{11}-x_{10})\]
\[f(x_1, x_{21})-f(x_1,x_{20}) = \alpha_2 (x_{21}-x_{20})\]
\(x_1\) 이 \(x_{10}\) 에서 \(x_{11}\) 으로 변할 때, 함수 $f$의 변화량은 \((x_{11}-x_{10})\), 즉 $x_1$의 변화량에 항상 비례한다. 그리고 $x_1$과 $x_2$가 모두 이런 제약을 만족하는 함수는 다음의 형태밖에 없다.

\[f(x_1, x_2) = \alpha_0 + \alpha_1 x_1 + \alpha_2 x_2\]

이 함수는 $x_1$과 \(x_2\) 의 선형 함수이다. 모수 \(\beta_0\), \(\beta_1\) 의 선형함수는 다음과 같은 형태를 띈다.

\[f(\beta_0, \beta_1) = \alpha_0 + \alpha_1 \beta_0 + \alpha_2 \beta_1\]