분위수 손실(Quantile loss)에 대한 직관적 이해
분위수 회귀(Quantile regression)
우리가 흔히 하는 회귀분석은 주어진 상황(예측 변수가 주어졌을 때), 결과 변수의 평균을 예측한다. 이에 반해 Quantile regression은 예측 변수가 주어졌을 때, 결과 변수의 q-분위수를 예측한다.
어떤 확률변수 \(Y\) 가 있을 때, q-분위수는 다음의 조건을 만족한다.
\[P(Y < y_{(q)}) = q\]
다시 말해 확률변수 \(Y\) 의 0.7-분위수는 확률변수 \(Y\) 가 0.7-분위수보다 작을 확률이 0.7이다. 0.7-분위수는 확률변수 \(Y\) 의 분포를 0.7대 0.3으로 가르는 수라고 생각할 수 있다. (표준정규분포에서 -1.96과 1.96은 0.025-분위수와 0.975-분위수이다.)
qnorm(p=c(0.025, 0.975), mean=0, sd=1)
## [1] -1.959964 1.959964
quantile regression은 조건부 분위수를 추정한다고 생각하면 된다.
\[P(Y< y_{(q)}(x) | X = x) = q\]
위의 식은 예측 변수가 \(x\) 로 주어졌을 때, 확률변수 \(Y\) 의 \(q\) -분위수 \(y(q)\) 에 대한 정의를 나타낸다. 확률변수 \(Y\) 의 \(q\) -분위수는 예측 변수 \(x\) 의 값에 따라 달라질 수 있으므로 \(x\) 의 함수 \(y_{(q)}(x)\) 로 나타내었다.
분위수 손실(Quantile loss)
그런데 q-분위수를 어떻게 추정해야 할까?
잠시 <기초 통계학의 숨은 원리>란 책을 살펴보자.
링크 : <기초 통계학의 숨은 원리 발췌: 왜 표본중앙값이 아니라 표본평균인가?>
결론적으로 0.5-분위수(중앙값)을 추정하기 위해서 MAE(Mean Absolute Error)를 많이 쓴다. 왜냐하면 MAE를 최소로 하는 추정량은 표본 중앙값(표본에서 0.5-분위수)이기 때문에 일치(Consistent)추정량(표본 크기가 매우 클 때에 모수에 거의 확실히 수렴하는 추정량)이라고 생각할 수 있다.
물론 특정한 분포를 가정한다면 표본 중앙값보다 더 효율적인 추정량을 구할 수 있겠지만, 우리는 분포를 모른다!
반면 q-분위수를 추정할 때에는 다음과 같은 Loss를 최소화하는 값을 추정값으로 사용한다.
\[L(y_{(q)},q, \vec{y}) = \sum (q-\mathbb{I}(y_i-y_{(q)} > 0))(y_i-y_{(q)})\]
처음 이 식을 봤을 때, 왜 이래야 하는지 굉장히 헷갈렸다. 온통 수식으로 도배되어 있는 논문을 봤을 때에도 혼란스럽기 그지 없었다. “하지만 수식의 장벽을, 채 100개도 되지 않는 수학 기호를 넘어, 그 뒤에 숨겨 있는 이유와 의미를 이해하면, 여러분은 더 많은 자유와 여유를 누릴 수 있습니다.”
자, 위에서 표준 중앙값을 구할 수 있는 손실 함수를 확인했다. 손실 함수를 MAE로 하며, MAE를 최소화하는 값은 표본 중앙값이 된다.
여기서 표본 0.9-분위수를 구하는 방법, 0.9-분위수를 구할 수 있는 손실함수를 생각해보자.
중앙값은 그 수(중앙값)보다 작은 수의 갯수와 그 수보다 큰 수의 갯수가 정확히 1:1이 되는 수이다.
반면 0.9-분위수는 그 수(0.9-분위수)보다 작은 수의 갯수가 그 수보다 큰 수의 갯수보다 9배인 수이다.
그렇다면 그 수보다 큰 수들은 9배를 해주면, 양쪽의 갯수가 동등해지지 않은가?
아주 간단한 예를 들어 보자. 다음에 표본이 있다.
\(1, 2, 3, 4, 5, 6, 7, 8, 9, 10\)
여기서 \(5.5\) (또는 그 근방의 수)는 위의 수를 정확히 1:1로 나눈다.
\(9.5\) 는 위의 수를 정확히 9:1로 나눈다. 이때 10를 9개 늘려줘보자.
\(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 10, 10, 10, 10, 10, 10, 10, 10\)
위의 새로운 표본에 대해 중앙값을 구하면 \(9.5\) 가 된다.
다시 말해 어떤 표본에서 표본 q-분위수의 특징을 알 수 있다.
q-분위수보다 작은 수와 큰 수의 비가 \(q:(1-q)\) 가 되어야 한다.
그리고 q-분위수는 q-분위수보다 작은 수와 큰 수에 대해 \((1-q)\) 와 \(q\) 의 비중(weight)를 곱해 줬을 때, 중앙값에 해당한다!
위의 식에서 \(\mathbb{I}(y_i-y_{(q)} > 0)\) 는 Indicator 함수로 \(y_i-y_{(q)}>0\) 가 만족하면 1, 아니면 0이 된다. 따라서 \((q-\mathbb{I}(y_i-y_{(q)} > 0))\) 는 \(y_i\) 와 \(y_{(q)}\) 의 상대 크기에 따라 \(q\) 또는 \((q-1)\) 이 된다. \((q-1)\) 에 \(-1\) 을 곱하면 \((1-q)\) 가 된다. \(-1\) 은 \((y_i-y_{(q)})\) = \(-|(y_i-y_{(q)})|\) (if \((y_i-y_{(q)} < 0\) ) 에서 공급된다!
위의 손실함수를 간단히 \(y_i-y{(q)}> 0\) 일 때, \(q|(y_i-y_{(q)})|\) , \(y_i-y{(q)} \leq 0\) 일 때, \((1-q)|(y_i-y_{(q)})|\) 로 나타내기도 한다.
그냥 정렬해서 구하지?
그런데 왜 이렇게 복잡하게 구하지? 그냥 정렬해서 자르면 되지 않은가?
하지만 정렬하는 방법은 quantile regression에 적용하기 힘들지 싶다. 다시 말해 \(Y_{(q)}\) 를 구할 순 있어도, \(Y_{(q)}|X\) 를 구하긴 힘들어 보인다.
결론
quantile loss는 q-분위수를 찾기 위해 특별히 고안된 weighted MAE라고 이해할 수 있다. 보통 weighted loss는 어떤 자료에 대해 weight이 정해지지만 quantile loss의 weight은 q-분위수 추정값에 따라 \(q\) 또는 \(1-q\) 로 달라지는 weight이라고 생각할 수 있다!!!
PS
마지막으로 quantile-gam의 예로 글을 마치고자 한다. 다음은 데이터와 qgam패키지를 사용하여 예측한 conditional 0.2, 0.4, 0.6, 0.8-quantile을 보여준다. (참고 : https://mfasiolo.github.io/qgam/articles/qgam.html )
데이터는 R 플롯 팁에서 가져왔다.
library(qgam); library(MASS)
library(data.table)
if( suppressWarnings(require(RhpcBLASctl)) ){ blas_set_num_threads(1) } # Optional
N <- 7000
x1 <- rnorm(N/2)
y1 <- 2*sin(x1) + rnorm(N/2)
x2 <- rnorm(N/2)
y2 <- 2*cos(x2) + rt(N/2, df=30)
dat <- data.frame(x=c(x1,x2),
y=c(y1,y2))
quSeq <- c(0.2, 0.4, 0.6, 0.8)
set.seed(6436)
fit <- mqgam(list(y~ s(x, k=20, bs="ad"), ~ s(x)),
data = dat,
qu = quSeq)
# Plot the data
xSeq <- data.frame(x = seq(-4, 4, length.out = 1e3))
#plot(dat$x, dat$y, xlab = "x", ylab = "y", xlim=c(-3,3))
datPred <- data.frame(q = rep(quSeq, each=nrow(xSeq)),
x = xSeq$x,
y = NA)
for(iq in quSeq) {
datPred[datPred$q == iq, 'y'] = qdo(fit, iq, predict, newdata = xSeq)
#lines(xSeq$x, pred, col = 2)
}
datPred$q = factor(datPred$q, levels = c(0.8, 0.6, 0.4, 0.2))
library(ggplot2)
#png('qloss-qgam.png', width=480, height=360)
ggplot() +
geom_point(data=dat, mapping=aes(x=x, y=y), alpha=0.3) +
geom_line(data=datPred, mapping=aes(x=x, y=y, color=q),
size=1.1)
#dev.off()
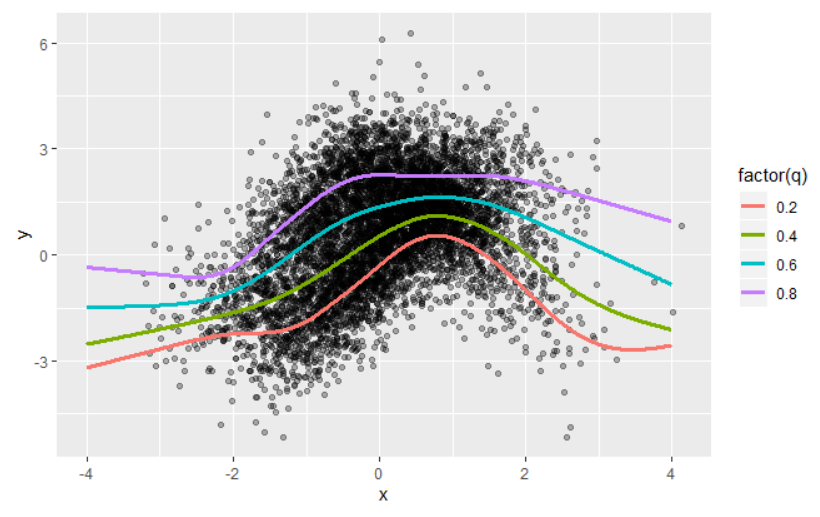
위의 그림을 보고 있자니 Mixture Density에는 어떻게 적용될지 궁금해졌다.
# quantiles = 0.05 - 0.95
quSeq <-seq(0.05, 0.95, 0.05)
#quSeq <-seq(0.1, 0.9, 0.1)
set.seed(6436)
fit <- mqgam(list(y~ s(x, k=20, bs="ad"), ~ s(x)),
#fit <- mqgam(y~ s(x, k=20, bs="ad"),
data = dat,
qu = quSeq)
# Plot the data
xSeq <- data.frame(x = seq(-15, 15, length.out = 1e3))
#plot(dat$x, dat$y, xlab = "x", ylab = "y", xlim=c(-3,3))
datPred <- data.frame(q = rep(quSeq, each=nrow(xSeq)),
x = xSeq$x,
y = NA)
for(iq in quSeq) {
datPred[datPred$q == iq, 'y'] = qdo(fit, iq, predict, newdata = xSeq)
#lines(xSeq$x, pred, col = 2)
}
#datPred$q = factor(datPred$q, levels = rev(quSeq))
library(ggplot2)
library(colorspace)
#png('qloss-qgam.png', width=480, height=360)
ggplot() +
geom_point(data=dat, mapping=aes(x=x, y=y), alpha=0.3) +
geom_line(data=datPred, mapping=aes(x=x, y=y, color=q, group=q),
size=1.1) +
#scale_color_continuous('RdBl')
#scale_color_continuous_sequential('Viridis', begin=0, end=0.7)
scale_color_continuous_sequential('Viridis')
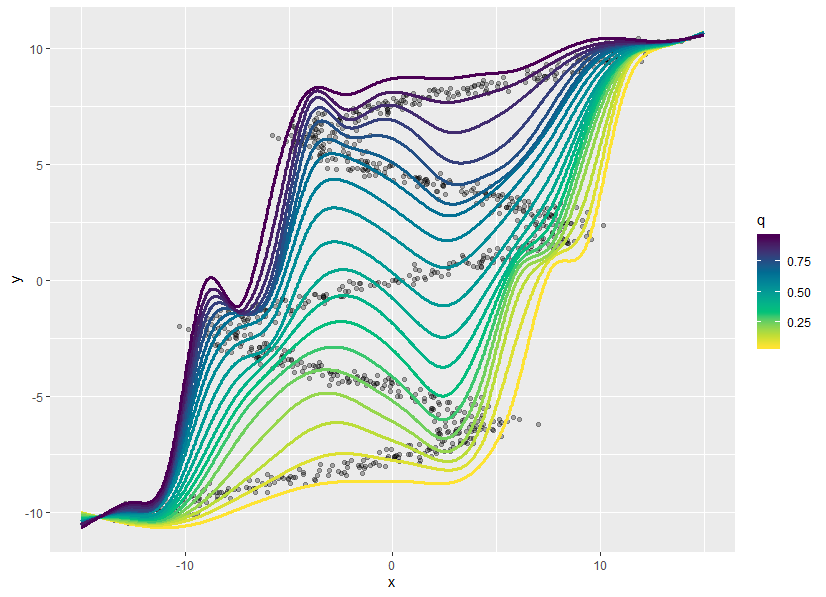
다음에는 Quantile Neural Network를 적용해봐야겠다.
admin
구현했다.
https://github.com/maxmarketit/Auto-PyTorch/blob/develop/examples/quantiles/Quantiles.ipynb