내생성(Endogeneity)
내생성(Endogeneity)
내생성은 (선형 모형에서) 설명변수와 오차항의 상관이 0이 아닌 경우를 의미한다. 계량경제학(Econometrics)에서 주로 사용하는 용어인 내생성은 실험을 주로 하는 자연과학이나 심리학과 학생들은 들어보지도 못한 경우도 많을 것이다.
만약 선형 모형이 다음과 같다고 하자.
\[ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots \beta_p x_p + e\]
이때 설명변수 \(x_i\) 에 내생성이 존재한다는 것은 다음과 같이 수식으로 나타낼 수 있다.
\[\textrm{cov}(x_i, e) \neq 0\]
좀 더 흔하게 \(\mathbb{E}[x_i e] \neq 0\) 으로 쓰기도 한다.
이 둘은 (거의) 같은 의미이다. \(\textrm{cov}(x_i, e) = \mathbb{E}[x_i e] – \mathbb{E}[x_i] \mathbb{E}[e]\) 에서 만약 \(\mathbb{E}[e] = 0\) 이라면 \(\textrm{cov}(x_i, e) = \mathbb{E}[x_i e]\) 이기 때문이다. (그리고 \(\mathbb{E}[e]=0\) 이다! 만약 0이 아니라면 그것을 절편에 포함시켜서 0으로 만들 수 있다.)
이때 주의해야 한다! 위의 모형은 인과관계(causal relation)을 나타내는 모형이다. 우리가 흔히 배우는 다음의 선형모형과는 다른다!
\[y = \beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p + e, \ \ e \sim \mathcal{N}(0, \sigma^2)\]
\[\mathbb{E}(y|x_1, x_2, \cdots, x_p) = \beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p \]
예측 모형 vs. 인과 관계(원인-결과) 모형
위의 선형 관계 모형은 우리가 관심을 가지고 있는 설명 변수 \(x_i\) 가 실험상황에서 무작위로 배정한 경우일 때 인과관계를 나타낸다. (이렇게 무작위로 배정한 경우 확률적으로 \(x_i\) 와 \(e\) 는 서로 독립이 된다.) 흔히 하는 가장 단순한 실험인 실험군과 대조군을 비교하는 실험 자료를 생각해보자. 실험군 여부를 나타내는 설명 변수(이런 경우에는 독립 변수라고 쓰기도 한다) \(x_i\) 의 계수는 대조군의 조건을 실험군의 조건을 바꿈에 따라서 나타나는 결과 변수의 차이를 나타낸다. 다시 한 번 정확하게 말해보자. \(x_i\) 의 계수는 동일한 개체의 실험 조건을 바꿈에 따라 예상되는 결과 변수의 변화량을 나타낸다.
하지만 관찰 자료에 대해 선형회귀분석을 했을 경우에는 어떤 설명 변수 \(x_i\) 의 계수는 원인-결과(인과) 관계를 나타내지 못한다. 단지 모집단에서 회귀 모형의 다른 변수들은 동일하지만 특정한 설명 변수 \(x_i\) 는 1만큼 큰 다른 개체를 관찰했을 때 예상할 수 있는 결과 변수의 차이를 나타낸다.
이 둘의 차이는 심오하고도 언뜻 이해하기 어렵지만, 내생성을 이해하는 핵심이다!
Pearl의 표기법을 따른다면, 첫 번째 계수와 두 번째 계수는 다음과 같이 나타낼 수 있다. (Pearl을 읽은지 오래라 확실하진 않다.)
- 첫 번째 계수 : \(\beta_i = \mathbb{E}[y | x_1, \cdots, \mathrm{do}(x_i \leftarrow \xi + 1), \cdots, x_p] – \mathbb{E}[y | x_1, \cdots, x_i=\xi, \cdots, x_p]\)
- 두 번째 계수 : \(\beta_i = \mathbb{E}[y | x_1, \cdots, x_i+1, \cdots, x_p] – \mathbb{E}[y | x_1, \cdots, x_i, \cdots, x_p]\)
예측 모형과 인과관계 모형의 차이 : 조건부 오차항 평균
내가 가장 이해하기 어려웠던 것은 사실 내생성의 정의라고 할 수 있는 \(\textrm{cov}(x_i, e) \neq 0\) 였다.
가장 기본적인 선형 회귀모형에 따르면, \(y = \beta_0 + \beta_1 x_1 + e\) 에서 \(e \sim \mathcal{N}(0, \sigma^2)\) 이기 때문에 \(e\) 는 \(\mathbb{E}[e]=0\) 이고, \(\mathbb{E}[e|x_1]=0\) 이다. 두 번째 수식은 어떠한 \(x_1\) 에 대해서도 \(e\) 의 조건부 평균은 0임을 의미한다.
하지만 \(\textrm{cov}(e, x_i) \neq 0\) 이라면 얘기는 달라진다. 만약 공분산이 양이라면, \(x_i\) 가 평균보다 큰 경우에 \(e\) 는 평균보다 큰 경향을 보인다. 다시 말해 평균보다 큰 \(x_i\) 에 대해 \(\mathbb{E}[e | x_i]\) 는 0보다 클 확률이 높다!
근데 계수 추정은 \(\mathbb{E}[e | x_i]=0\) 을 가정하지 않는가?
인과 관계 모형에서의 조건부 오차항 평균은 0이 아닐 수 있다.
이는 인과 관계 모형과 예측 모형을 명시적으로 구별하여 얘기하지 않아서 일어나는 혼동이다. 인과관계 모형에서 오차항 \(e\) 는 인과관계를 제외하고 결과 변수를 결정짓는 모든 부분을 의미한다. 따라서 \(\mathbb{E}[e | x_1, x_2, \cdots, x_p]\) 는 0이 아닐 수도 있다.
다음의 예시를 보자.
예시: 농구 선수의 기량
예를 들어 어떤 농구 선수의 기량이 키와 근력으로 결정난다고 생각해보자. (이는 인과관계 모형이다.)
\[\textrm{ability} = \beta_0 + \beta_1 \textrm{height} + \beta_2 \textrm{power} + e\]
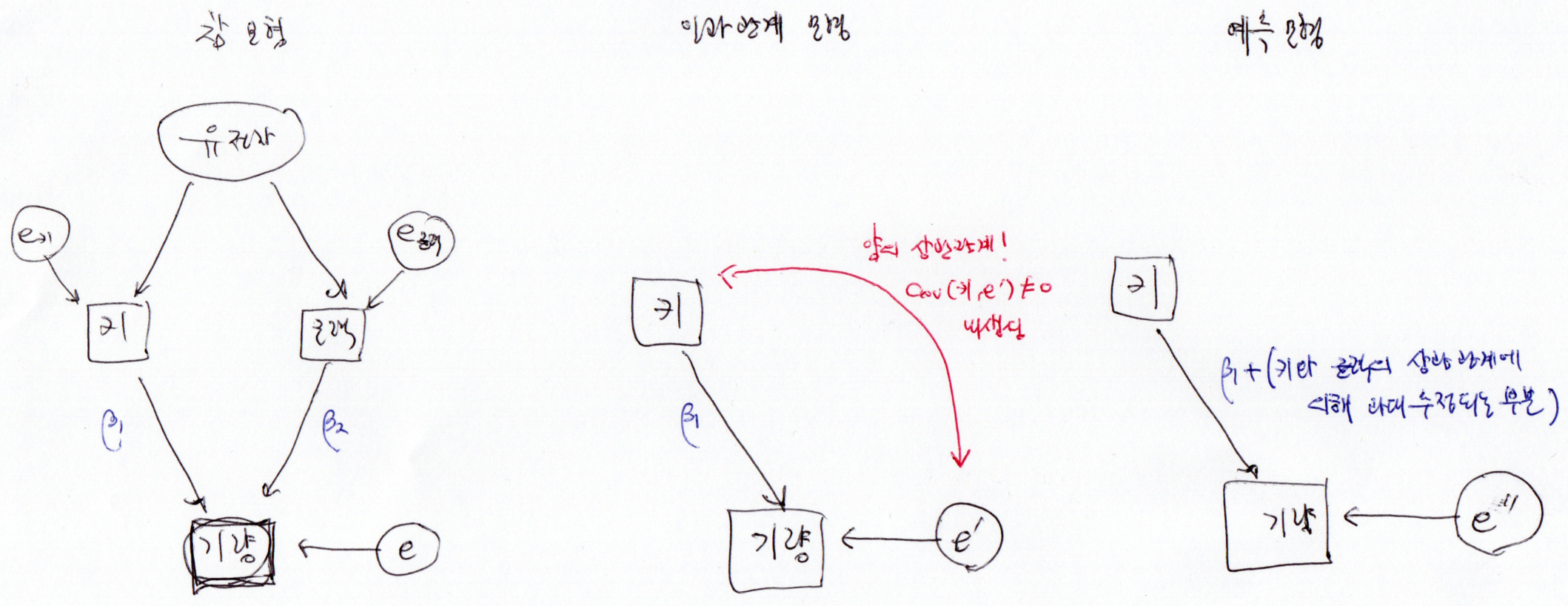
여기서 키( \(\textrm{height}\) )과 근력( \(\textrm{power}\) )은 상관관계가 있다. 그리고 인과적으로 볼 때 이는 공통의 유전자( \(\textrm{gene}\) )가 키와 근력에 관계하기 때문이다. 이 유전자에 의해 큰 키의 선수는 대체로 근력도
평균보다 강한 경향이 있다.
이런 상황에서 기량( \(\textrm{ability}\) )에 대해 인과관계 모형을 키( \(\textrm{height}\) )만을 사용해서 나타내면 다음과 같다.
\[\textrm{ability} = \beta_0 + \beta_1 \textrm{height} + e’\]
그리고 위의 식에서 \(e’\) 는 앞 선 식에서 \(\beta_2 \textrm{power} + e\) 와 같다. 앞에서 근력은 키와 상관 관계가 있다고 했으므로, 인과관계 모형 \(\textrm{ability} = \beta_0 + \beta_1 \textrm{height} + e’\) 에서 설명변수 \(\textrm{height}\) 와 오차항 \(e’\) 에는 상관관계가 존재한다.
만약 동일한 자료를 예측 모형으로 나타내면 다음과 같다.
\[\textrm{ability} = \beta_0 + {\beta_1}‘ \textrm{height} + {e’}‘\]
여기서 \({e’}‘\) 는 앞의 \(e\) 또는 \(e’\) 과 다른 값을 나타내기 마련이고, \(\beta_1’\) 역시 \(\beta_1\) 보다 커지는 경향이 있다. (여기서는 키와 근력이 양의 상관관계를 가진다는 가정을 하였다.) 왜냐하면 인과관계 모형 \(\textrm{ability} = \beta_0 + \beta_1 \textrm{height} + \beta_2 \textrm{power} + e\) 에 따르면 기량은 키와 근력에 의해 좌우되는데, 키가 큰 사람들은 근력도 강하기 때문에 키의 향상( \(\beta_1\) )과 근력 향상( \(\beta_2\) )에 따른 기량 향상의 효과를 모두 누리기 때문이다. 하지만 어떤 사람이 키만을 증가시켰을 때 기대되는 기량의 향상은 \(\beta_1\) 뿐이다(여기서는 인위적으로 키를 증가시키는 방법이 있다고 가정하였다. 키높이 농구화라던지…).
백문이 불여일견이라고 다음의 시뮬레이션을 보자.
set.seed(1)
N <- 1000
gene <- rnorm(N)
power <- gene + rnorm(N)
height <- 180 + 5*gene + rnorm(N)
ability <- power + height/10 + rnorm(N)
summary(lm(ability ~ height)) # 예측 모형
## ## Call: ## lm(formula = ability ~ height) ## ## Residuals: ## Min 1Q Median 3Q Max ## -5.1616 -1.0461 -0.0145 1.0365 5.0071 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -35.56398 1.59503 -22.30 <2e-16 *** ## height 0.29756 0.00886 33.59 <2e-16 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 1.491 on 998 degrees of freedom ## Multiple R-squared: 0.5306, Adjusted R-squared: 0.5301 ## F-statistic: 1128 on 1 and 998 DF, p-value: < 2.2e-16
summary(lm(ability ~ height + power)) # 원인 결과 모형
## ## Call: ## lm(formula = ability ~ height + power) ## ## Residuals: ## Min 1Q Median 3Q Max ## -3.2322 -0.7124 -0.0099 0.7173 3.0623 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -0.372789 1.551017 -0.24 0.81 ## height 0.102167 0.008614 11.86 <2e-16 *** ## power 1.013926 0.031168 32.53 <2e-16 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 1.039 on 997 degrees of freedom ## Multiple R-squared: 0.7723, Adjusted R-squared: 0.7718 ## F-statistic: 1691 on 2 and 997 DF, p-value: < 2.2e-16
위의 결과를 보면 예측 모형에서 \(\textrm{height}\) 의 계수는 원인-결과 모형의 참계수 0.1을 과대 추정하고 있을 볼 수 있다. 하지만 두 번째 결과를 보면 설명변수로 \(\textrm{ability}\) 를 추가했을 경우에는 동일한 추정방법(OLS; Ordinary Least Squares)을 사용하였지만 원인-결과 모형의 계수를 거의 정확하게 추정하고 있음을 볼 수 있다.
중간 정리
이 글의 핵심은 다음과 같다.
관찰 자료에서 원인-결과 모형의 계수를 추정하려면 내생성이 없어야 한다.
그리고 실험을 주로 하는 학과에서 내생성에 큰 주의를 주지 않는 이유는 주로 다루는 자료가 실험 자료이기 때문이다. 실험 자료에서는, 특히 무작위 대조군 연구를 하였다면, 내생성이 존재할 가능성이 적기 때문이다.
반면, 경제학처럼 관찰 자료를 통해 인과 관계 모형을 추정하는 곳에서는 내생성을 효과적으로 대처할 수 있는 방법이 필수적이다.
내생성이 대처하는 방법
- 위에서 인과 관계가 있는 모든 변수(키, 근력)을 모두 회귀 모형에 넣은 것처럼 관련된 통제 변수를 회귀 모형에 추가한다.
- 도구 변수(Instrumental Variable)을 활용한다. 여기서 도구 변수란 내생성 있는 설명변수와 상관관계가 있지만, 오차항과는 상관관계가 없는 변수를 의미한다.
- SEM(Structural Equation Modeling) 또는 GSEM(Generalized Structural Equation Modeling)을 활용하여 오차 상관을 모형화한다.
- GMM(Generalized Method of Moments)를 활용한다.
정리/요약
-
인과관계 모형과 예측 모형은 다르다! 특히 오차항이 다르다. 인과관계 모형에서 오차항은 인과 관계로 설명되는 부분을 제외한 모든 부분이다. 반면 예측모형에서는 오차항은 설명변수로 예측할 수 있는 부분을 제외한 모든 부분이다.
-
인과관계 모형에서 인과 관계 변수와 오차항에 상관이 있을 때 그 변수에 내생성(Endogeneity)이 존재한다고 한다. 내생성은 다음과 같이 정의한다. 인과관계 변수 \(x_i\) 에 대해, \(\textrm{cov}(x_i, e) \neq 0\) .
-
관찰 자료를 통해 인과관계 모형을 추정할 때에 OLS를 사용하면 내생성(Endogeneity)에 의해 인과관계를 과대/과소 추정할 수도 있다.
Leave a comment