경로 분석
경로 분석은 인과 관계를 밝혀낼 수 있는가?
사람들이 오해하는 것 중의 하나가 경로 분석 또는 구조방정식모형을 사용하면 자동적으로 인과관계를 알아낼 수 있다고 생각하는 것이다.
반대쪽의 극단으로는 관찰 데이터로는 절대 인과 관계를 밝힐 수 없다고 주장하는 사람들이 있다.
하지만 이론적으로 모형이 정확하다면 관찰 데이터로도 인과관계를 밝힐 수 있다. (그런데 많은 사람들이 모형을 정확하게 만드는 것이 얼마나 어려운지 잘 모른다는 것이 함정이다.)
앞선 예시를 다시 보자.
예시: 유전자-키-근력-기량의 관계
(지난 글과 동일합니다.)
예를 들어 어떤 농구 선수의 기량이 키와 근력으로 결정난다고 생각해보자. (이는 인과관계 모형이다.)
\[\textrm{ability} = \beta_0 + \beta_1 \textrm{height} + \beta_2 \textrm{power} + e\]
여기서 키( \(\textrm{height}\) )과 근력( \(\textrm{power}\) )은 상관관계가 있다. 그리고 인과적으로 볼 때 이는 공통의 유전자( \(\textrm{gene}\) )가 키와 근력에 관계하기 때문이다. 이 유전자에 의해 큰 키의 선수는 대체로 근력도
평균보다 강한 경향이 있다.
이런 상황에서 기량( \(\textrm{ability}\) )에 대해 인과관계 모형을 키( \(\textrm{height}\) )만을 사용해서 나타내면 다음과 같다.
\[\textrm{ability} = \beta_0 + \beta_1 \textrm{height} + e’\]
그리고 위의 식에서 \(e’\) 는 앞 선 식에서 \(\beta_2 \textrm{power} + e\) 와 같다. 앞에서 근력은 키와 상관 관계가 있다고 했으므로, 인과관계 모형 \(\textrm{ability} = \beta_0 + \beta_1 \textrm{height} + e’\) 에서 설명변수 \(\textrm{height}\) 와 오차항 \(e’\) 에는 상관관계가 존재한다.
만약 동일한 자료를 예측 모형으로 나타내면 다음과 같다.
\[\textrm{ability} = \beta_0 + {\beta_1}‘ \textrm{height} + {e’}‘\]
여기서 \({e’}‘\) 는 앞의 \(e\) 또는 \(e’\) 과 다른 값을 나타내기 마련이고, \(\beta_1’\) 역시 \(\beta_1\) 보다 커지는 경향이 있다. (여기서는 키와 근력이 양의 상관관계를 가진다는 가정을 하였다.) 왜냐하면 인과관계 모형 \(\textrm{ability} = \beta_0 + \beta_1 \textrm{height} + \beta_2 \textrm{power} + e\) 에 따르면 기량은 키와 근력에 의해 좌우되는데, 키가 큰 사람들은 근력도 강하기 때문에 키의 향상( \(\beta_1\) )과 근력 향상( \(\beta_2\) )에 따른 기량 향상의 효과를 모두 누리기 때문이다. 하지만 어떤 사람이 키만을 증가시켰을 때 기대되는 기량의 향상은 \(\beta_1\) 뿐이다(여기서는 인위적으로 키를 증가시키는 방법이 있다고 가정하였다. 키높이 농구화라던지…).
두 가지 모형
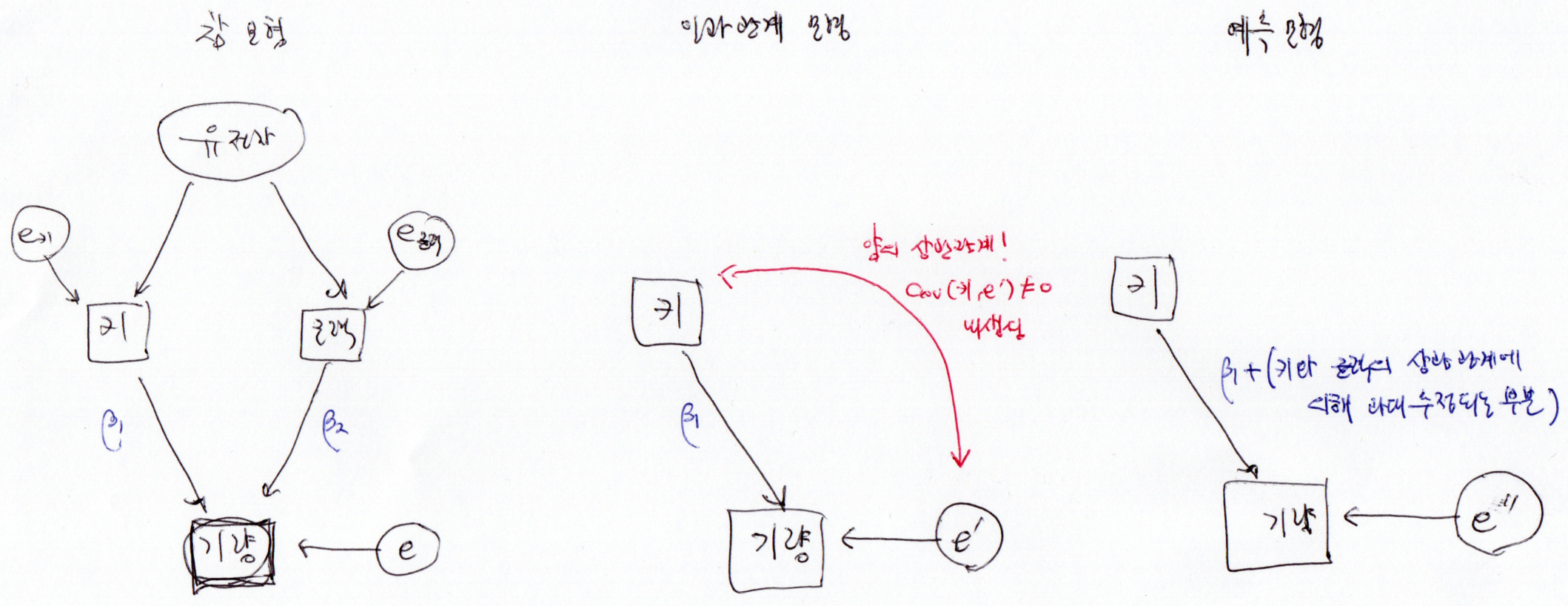
인과관계 모형
앞에서 글에서 설명했듯이 예측 모형은 키와 오차의 상관관계를 0으로 놓고 키로 설명할 수 있는 모든 부분을 키의 회귀 계수로 추정한다. 만약 내생성(설명변수와 오차의 상관관계)이 존재한다면 이 추정값은 인과관계 계수을 과대 혹은 과소 추정하게 된다.
만약 설명변수와 오차의 공분산을 알고 있다면, 경로분석을 써서 이를 모형에 반영할 수 있다. 다음을 보자.
set.seed(1)
N <- 1000
gene <- rnorm(N)
power <- gene + (e1 = rnorm(N))
height <- 180 + 5*gene + (e2 = rnorm(N))
ability <- power + height/10 + (e3 = rnorm(N))
#summary(lm(ability ~ height)) # 예측 모형
#summary(lm(ability ~ height + power)) # 원인 결과 모형
cov(height, power + e3)
## [1] 5.604122
시뮬레이션 자료에 존재하는 키와 인과관계 오차와의 공분산은 5.6이다. 이를 반영하여 모형을 구성하고 경로 분석을 실시해보자.[1]
[1] : 물론 실제 상황에서 설명변수와 오차의 공분산을 정확히 알기 힘들 것이다.
causalModel <- '
ability ~ height
ability ~~ b4*height
b4 == 5.6'
dat = data.frame(gene=gene, power=power, height=height, ability=ability)
library(lavaan)
fit <- sem(causalModel, data=dat)
causalModel에서 ability ~~ b4*height는 ability의 오차와 height 사이에 공분산이 b4임을 나타내고, 다음 줄 b4==5.6은 이 공분산을 5.6으로 고정시켜 두었다.
summary(fit)
## lavaan 0.6-3 ended normally after 17 iterations ## ## Optimization method NLMINB ## Number of free parameters 4 ## Number of equality constraints 1 ## ## Number of observations 1000 ## ## Estimator ML ## Model Fit Test Statistic 0.000 ## Degrees of freedom 0 ## ## Parameter Estimates: ## ## Information Expected ## Information saturated (h1) model Structured ## Standard Errors Standard ## ## Regressions: ## Estimate Std.Err z-value P(>|z|) ## ability ~ ## height 0.100 0.013 7.991 0.000 ## ## Covariances: ## Estimate Std.Err z-value P(>|z|) ## .ability ~~ ## height (b4) 5.600 ## ## Variances: ## Estimate Std.Err z-value P(>|z|) ## .ability 3.326 0.111 29.988 0.000 ## height 28.338 1.267 22.361 0.000 ## ## Constraints: ## |Slack| ## b4 - (5.6) 0.000
분석 결과를 보면 Regressions: ability~height의 계수가 0.1로 인과관계 계수를 정확하게 추정하고 있다.(이렇게 정확한 것은 공분산을 실제 자료에서 계산했기 때문이다. 보통의 경우에는 공분산을 정확하게 알지 못하므로 이 정도로 정확하게 추정하지 못한다.)
예측 모형
사실 예측 모형도 인과관계 모형과 크게 다르지 않다.
predModel <- '
ability ~ height
ability ~~ b4*height
b4 == 0'
library(lavaan)
fit2 <- sem(predModel, data=dat)
summary(fit2)
## lavaan 0.6-3 ended normally after 12 iterations ## ## Optimization method NLMINB ## Number of free parameters 4 ## Number of equality constraints 1 ## ## Number of observations 1000 ## ## Estimator ML ## Model Fit Test Statistic 0.000 ## Degrees of freedom 0 ## Minimum Function Value 0.0000000000000 ## ## Parameter Estimates: ## ## Information Expected ## Information saturated (h1) model Structured ## Standard Errors Standard ## ## Regressions: ## Estimate Std.Err z-value P(>|z|) ## ability ~ ## height 0.298 0.009 33.620 0.000 ## ## Covariances: ## Estimate Std.Err z-value P(>|z|) ## .ability ~~ ## height (b4) 0.000 ## ## Variances: ## Estimate Std.Err z-value P(>|z|) ## .ability 2.220 0.099 22.361 0.000 ## height 28.338 1.267 22.361 0.000 ## ## Constraints: ## |Slack| ## b4 - 0 0.000
단지 (인과관계를 보여줄 수 없는) 인과관계 모형으로 부적합한 모형일 뿐이다.
인과 관계를 알아내는 다른 방법들
만약 height와 오차의 상관관계를 정하지 않고 추정을 하려면 다음과 같은 결과가 나온다.
causalModel2 <- '
ability ~ height
ability ~~ b4*height
'
library(lavaan)
fit3 <- sem(causalModel2, data=dat)
## Warning in lav_model_vcov(lavmodel = lavmodel, lavsamplestats = lavsamplestats, : lavaan WARNING: ## Could not compute standard errors! The information matrix could ## not be inverted. This may be a symptom that the model is not ## identified.
이런 이유로 지난 번 시간에 내생성에 대처하는 방법들이 필요하다. 아래의 세 번째 방법이 위에서 사용한 방법이다.[2] 결론적으로 말하면, 정보가 더 필요해! 쯤으로 정리할 수 있다.
[2] : 경로 분석은 구조방정식모형(SEM; Structural Equation Modeling)의 단순한 형태이다.
내생성이 대처하는 방법
- 위에서 인과 관계가 있는 모든 변수(키, 근력)을 모두 회귀 모형에 넣은 것처럼 관련된 통제 변수를 회귀 모형에 추가한다.
- 도구 변수(Instrumental Variable)을 활용한다. 여기서 도구 변수란 내생성 있는 설명변수와 상관관계가 있지만, 오차항과는 상관관계가 없는 변수를 의미한다.
- SEM(Structural Equation Modeling)[3] 또는 GSEM(Generalized Structural Equation Modeling)을 활용하여 오차 상관을 모형화한다.
- GMM(Generalized Method of Moments)를 활용한다.
[3] : SEM이란 약어를 쓰는 용어는 내가 아는 것만도 3개이다. 앞에서 설명한 교육학, 사회학, 심리학 등에서 많이 쓰는 구조방정식모형. 계량 경제학에서 사용하는 Simultaneous Equations Model(연립방정식 모형). 그리고 측정의 신뢰도와 밀접한 Standard Error of Measurement(측정표준오차).
Leave a comment