고정효과(fixed effect)와 임의효과(random effect)

분석 8월 05, 2019 3 Comments

고정효과(fixed effect)와 임의효과(random effect)

다른 분야, 다른 시기, 다른 용어

용어란 분야, 시기마다 다르게 사용되기 마련이다. 따라서 같은 용어가 다른 분야에서도 당연히 같은 의미를 가진다고 생각하는 것은 슬기롭지 못하다. 옛말로 어리다. (‘슬기롭지 못하고 둔하다’란 뜻을 가진 ‘어리석다’란 단어가 생기기 이전에는 ‘어리다’가 ‘어리석다’의 의미를 지니고 있었다.^[1] )

^{[1]^:} https://www.korean.go.kr/nkview/nknews/200503/80_1.html

통계학에서의 임의 효과

통계학에서 임의 효과(random effect)는 sampling of sampling의 맥락에서 쓰인다.

예를 들어 보자. 어떤 한 집단(모집단의 크기가 무한하다고 하자)의 키 평균(모평균)을 구하기 위해 사람의 키를 임의로 표집(sampling)하여 키 평균을 추정할 수 있다.

하지만 키를 측정하는 도구가 매우 조잡해서 측정된 키의 표준오차가 \(10\) cm 라고 가정해보자. 이때 측정에 따른 오차가 서로 독립이라면, 측정의 정확성을 높이는 것은 여러번 측정하는 것이다.

\(Y_{ij}\) : \(i\) 번째 사람의 \(j\) 번째 키 측정 결과
\(e_{ij}\) : \(i\) 번째 사람의 \(j\) 번째 키 측정에서 오차
\(\mu\) : 모평균(키)
\(\mu_i\) : \(i\) 번째 사람의 실제 키
\(Y_{ij} = \mu_i + e_{ij} = \mu + u_i + e_{ij}\) ( \(\mu\) : 전체 평균, \(u_i = \mu_i – \mu\) : \(i\) 번째 사람 실제 키와 전체 평균의 차이)

데이터가 어떻게 생성되는 살펴보자. 먼저 \(n\) 명의 키 측정 자료를 활용한다면,

sNum = 4
set.seed(sNum)
muAll = 175; sigmaAll = 15
n = 10
mu = rnorm(n, muAll, sigmaAll) # n 명의 표본 추출

t.test(mu)

## 
##  One Sample t-test
## 
## data:  mu
## t = 36.936, df = 9, p-value = 3.874e-11
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  172.2595 194.7364
## sample estimates:
## mean of x 
##  183.4979

모평균은 183(95% 신뢰구간 172.9-194)으로 추정되었다. 만약 여러 번 측정할 수 있다면,

sNum = 5
set.seed(sNum)
muAll = 175; sigmaAll = 15
n = 10;
ns = sample(5:10,n,replace=TRUE)
mu = rnorm(n, muAll, sigmaAll) # n 명 표본 추출
# 키 반복 측정(횟수, ns)
y <- g <- mus <-  vector("list", n)
for (i in 1:length(mus)) {
  mus[[i]] <- rep(mu[i], each=ns[i])
  y[[i]] <- rnorm(ns[i], mu[i], 10) # ns[i] 번 반복 측정
  g[[i]] <- rep(i, each=ns[i]) 
}
y <- unlist(y)
g <- factor(unlist(g))
mus <- unlist(mus)
dat <- data.frame(mus, g, y)
head(dat)

##        mus g        y
## 1 165.9564 1 164.5665
## 2 165.9564 1 159.9832
## 3 165.9564 1 144.1167
## 4 165.9564 1 168.3646
## 5 165.9564 1 163.3628
## 6 165.9564 1 174.9615

# This is the title image.
#ggplot(dat, aes(x=g, y=y)) + 
#   geom_hline(yintercept=175, linetype='dotted') + 
#   geom_boxplot() + 
#   geom_point(alpha=0.2)

데이터는 위와 같은 구조를 가지게 된다.

이때 이런 구조를 고려하지 않고 모평균을 추정한다면, 다음과 같다. 평균 \(\mu\) 가 \(175\) 와 다른지 검정한다면, 95% 신뢰구간으로 보아 영가설( \(\mu = 175\) )는 기각된다.

t.test(dat$y, mu=175)

## 
##  One Sample t-test
## 
## data:  dat$y
## t = -2.8967, df = 76, p-value = 0.004924
## alternative hypothesis: true mean is not equal to 175
## 95 percent confidence interval:
##  166.9416 173.5081
## sample estimates:
## mean of x 
##  170.2248

만약 Random-effect 모형을 사용한다면 다음과 같다. 우리는 전체 평균( \(\mu\) )이 \(175\) 와 다른지 확인하려면 두 번째 방법으로 손쉽게 검정할 수 있다. 결과는 기각할 수 없다.

#library(lme4)
library(lmerTest)
(lmerMod <- lmer(y ~ 1|g, data=dat))

## Linear mixed model fit by REML ['lmerModLmerTest']
## Formula: y ~ 1 | g
##    Data: dat
## REML criterion at convergence: 588.7467
## Random effects:
##  Groups   Name        Std.Dev.
##  g        (Intercept) 10.896  
##  Residual              9.865  
## Number of obs: 77, groups:  g, 10
## Fixed Effects:
## (Intercept)  
##       169.7

summary(lmerMod)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: y ~ 1 | g
##    Data: dat
## 
## REML criterion at convergence: 588.7
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.28259 -0.47224  0.04513  0.70982  2.27324 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  g        (Intercept) 118.72   10.896  
##  Residual              97.32    9.865  
## Number of obs: 77, groups:  g, 10
## 
## Fixed effects:
##             Estimate Std. Error      df t value Pr(>|t|)    
## (Intercept)  169.679      3.635   9.093   46.67 3.85e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(lmerMod2 <- lmer(I(y-175) ~ 1|g, data=dat))

## Linear mixed model fit by REML ['lmerModLmerTest']
## Formula: I(y - 175) ~ 1 | g
##    Data: dat
## REML criterion at convergence: 588.7467
## Random effects:
##  Groups   Name        Std.Dev.
##  g        (Intercept) 10.896  
##  Residual              9.865  
## Number of obs: 77, groups:  g, 10
## Fixed Effects:
## (Intercept)  
##      -5.321

summary(lmerMod2)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: I(y - 175) ~ 1 | g
##    Data: dat
## 
## REML criterion at convergence: 588.7
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.28259 -0.47224  0.04513  0.70982  2.27324 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  g        (Intercept) 118.72   10.896  
##  Residual              97.32    9.865  
## Number of obs: 77, groups:  g, 10
## 
## Fixed effects:
##             Estimate Std. Error     df t value Pr(>|t|)
## (Intercept)   -5.321      3.635  9.093  -1.464    0.177

마지막 방법은 가중치를 활용하여 WLS를 실시하는 것이다. 같은 피험자의 키를 4번 측정한 경우와 1번만 측정한 경우, 4번 측정한 피험자의 키에 대한 가중치를 \(¼\) 로 낮춰 주는 것이다. (이에 비해 위의 t.test는 모든 가중치를 1로 주는 경우이다.) 앞의 Mixed effect 모형과 약간 다르지만 비슷한 결과를 보여준다.

library(dplyr)
newdat <- dat %>% group_by(g) %>% summarise(y = mean(y), n=n())

lmMod <- lm(y ~ 1, weights=n, data=newdat)
summary(lmMod)

## 
## Call:
## lm(formula = y ~ 1, data = newdat, weights = n)
## 
## Weighted Residuals:
##    Min     1Q Median     3Q    Max 
## -35.53 -27.70   1.19  12.24  70.87 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  170.225      3.679   46.27 5.14e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 32.28 on 9 degrees of freedom

#summary(lmMod)
confint(lmMod)

##                2.5 %   97.5 %
## (Intercept) 161.9033 178.5464

lmMod2 <- lm(I(y-175) ~ 1, weights=n, data=newdat)
summary(lmMod2)

## 
## Call:
## lm(formula = I(y - 175) ~ 1, data = newdat, weights = n)
## 
## Weighted Residuals:
##    Min     1Q Median     3Q    Max 
## -35.53 -27.70   1.19  12.24  70.87 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)   -4.775      3.679  -1.298    0.227
## 
## Residual standard error: 32.28 on 9 degrees of freedom

#summary(lmMod)
confint(lmMod2)

##                2.5 %   97.5 %
## (Intercept) -13.0967 3.546356

계량경제학에서의 고정효과와 임의효과

<최근 패널자료 연구의 동향>^[2] 에서는 임의효과와 고정효과를 다음과 같이 설명한다.

문: 임의효과 (random effects)와 고정효과 (fixed effects)란?

답: 오차항이 \(v_{it} = u_i +ε_{it}\) 일 때, 이 중 개체별 효과( \(u_i\) )가 어떠한 것인지 지칭하는 용어이다. \(u_i\) 가 독립변수들과 상관( \(i\) 에 걸친 상관)되어 있으면 이 개체별 효과를 고정효과라 한다. 독립변수들과 상관되어 있지 않은 개체별 효과를 임의효과라 한다. \(u_i\) 를 두고 “고정효과”이거나 “임의효과”라고 하는 것은 적절하지만, 모형이 고정효과라거나 임의효과라고 하는 것은 타당하지 않다. 하지만 \(u_i\) 가 임의효과(고정효과)로 간주되는 모형이라는 뜻에서 “임의효과 모형(고정효과 모형)”이라고 하는 것은 적절하다.

^{[2]^:} https://www.kli.re.kr/klips/downloadCnfrncSjIemFile.do?iemNo=480

다음 노트의 정의는 좀 더 흥미롭다.^[3] 특히 random effect와 fixed effect를 모두 random variable이라고 설명하고 있다.

^{[3]^:} https://www.schmidheiny.name/teaching/panel2up.pdf

In the random effects model, the individual-specific effct is a random variable that is uncorrelated with the explanatory variables.

In the fixed effects model, the individual-specific effect is a random variable that is allowed to be correlated with the explanatory variables.

여기서 the individual-specific effect란 위에서 개체별 효과라고 칭한 다음 식의 \(u_i\) 에 해당한다.

\[Y_{ij} = \beta_0 + x_{ij} \beta_1 + u_i + e_{ij}\]

이 모형에서 설명변수의 갯수를 늘리면 다음과 표기할 수 있다.

\[Y_{ij} = \beta_0 + x_{1ij} \beta_1 + x_{2ij} \beta_2 + \cdots + u_i + e_{ij}\]

이때 개체별 효과에 대해 좀 더 생각해보자. 어떤 개체별 효과가 고정 효과인지 아닌지는 개체별 효과가 독립변수와 상관이 있는지 아닌지에 의해 결정된다. 그런데 독립변수란 모형에 따라 달라지게 마련이다. 따라서 개체별 효과가 고정효과인지 아닌지는 개체별 효과 자체의 성질이라기 보다는 모형에 의해 결정되는 것이라고 볼 수 있다!

어쨋든 (전통적인?) 통계학과 계량통계학(또는 경제통계학)에서 이렇게 다른 의미로 용어를 사용하고 있음에도 교육자들은 이를 무시하고 있다. 솔직히 이건 교육자의 잘못이라고 생각한다. 자기 분야에서 쓰이는 의미만을 가르치는 것은 학생들의 이해를 저해하고, 오해를 증진시키고, 학문간의 협력을 어렵게 하고, 학문의 발전을 더디게 한다. 자세히 설명할 시간이 없더라도 다른 분야(솔직히 계량 경제학과 전통적인 통계학이 그렇게 먼 분야도 아니다!)에서는 어떻게 쓰이는지 언급이라도 해야 하지 않겠는가?

그리고 계량경제학에서 고정효과와 임의효과를 저렇게 설명하는 것도 솔직히 조금 맘에 와 닿지 않는다. 내생성 포스팅에서 언급했지만, 추정값의 의미가 무엇인지, 그리고 그것이 정확한 방법인지는 어떤 모형을 사용했는지에 따라 달라진다. 임의효과 모형은 개체별 효과와 오차항이 독립이라는 가정이 들어가 있기 때문에 가정이 성립하는 상황에서만 효과 추정량에 편이가 없다. 반면 고정효과 모형은 그런 가정이 없기 때문에 그런 가정이 없는 경우에도 추정량에 편이가 없다.

따라서 고정 효과란 고정 효과 모형을 써야 편향이 없이 추정값을 구할 수 있는 효과이고, 임의 효과란 개체별 효과와 오차항이 독립이어서 임의 효과 모형을 써도 편향 없이 추정값을 구할 효과라고 설명하는게 낫지 않을까?

예시 : 인과관계 추정(계량경제학)에서 고정효과와 임의 효과 구분이 중요한 이유

다음은 사람들의 키와 체중의 관계를 보여준다.

\[ \textrm{weight}_{ij} = \beta_0 + \beta_{1} \textrm{gender}_i + \beta_2 \textrm{height}_{ij} + u_{i} + e_{ij} \]

체중은 평균적으로 키가 1 증가할 때 \(\beta_2\) 만큼 증가한다. (여기서는 키가 변할 수 있다고 가정했다. 아니면, 키가 성장하고 있는 청소년 데이터라고 생각해도 무방하다.)

이때 \(\textrm{height}\) 와 \(\textrm{gender}\) 에 상관관계가 있다. (보통 남자의 키가 여자보다 크다.) 하지만 \(\textrm{height}_i\) 와 \(u_i\) (개체별 효과)에 상관이 없다면 임의 효과 모형으로 \(\beta_2\) 를 추정해도 \(\beta_2\) 의 추정량은 비편향(unbiased)이다.

하지만 위의 모형에서 \(\textrm{gender}_i\) 를 제거한다면, 모형은 다음과 같이 변한다.

\[ \textrm{weight}_{ij} = \beta_0 + \beta_2 \textrm{height}_{ij} + (\beta_{1} \textrm{gender}_i + u_{i}) + e_{ij} = \beta_0 + \beta_2 \textrm{height}_{ij} + u_i’ + e_{ij} \]

새로운 개체별 효과 \(u_i’\) 는 \(u_i’ = \beta_{1} \textrm{gender}_i + u_{i}\) 이므로, 새로운 개체별 효과 \(u_i’\) 와 \(\textrm{height}_{ij}\) 는 상관이 있다.

따라서 이 간단한(reduced) 모형에서 임의 효과 모형으로 \(\beta_2\) 를 추정하면, 추정량은 편향이 생긴다. 이런 경우에 계량경제학은 FE(fixed effects) 모형을 쓰라고 가르킨다. 다음의 시뮬레이션은 각각의 모형에서 \(\beta_2\) 의 분포를 보여준다.

RE(Random effects) full 모형( \(\textrm{weight}_{ij} = \beta_0 + \beta_{1} \textrm{gender}_i + \beta_2 \textrm{height}_{ij} + u_{i} + e_{ij}\ \ (u_i \sim \mathcal{N}(0, \sigma_u^2))\) )
RE(Random effects) reduced 모형( \(\beta_0 + \beta_2 \textrm{height}_{ij} + u_i’ + e_{ij}\ \ (u_i’ \sim \mathcal{N}(0, \sigma_u^2))\) )
FE(Fixed effects) 모형( \(\beta_0 + \beta_2 \textrm{height}_{ij} + u_i’ + e_{ij}\) )

# SIMULATION
sNum = 11
set.seed(sNum)

# set nexp here ex) nexp=5000

res <- matrix(NA, nexp, 3)
res2 <- matrix(NA, nexp, 3)
colnames(res) <- c("random_full", "random_reduced", "fixed")
colnames(res2) <- c("random_full", "random_reduced", "fixed")

for (iexp in 1:nexp) {

  n =50;
  ns = sample(3:5, n, replace = TRUE) # length(ns)
  gender = sample(0:1, n, replace = TRUE) # length(gender)
  height = rnorm(n, 160, 10) + gender*10 # length(height)
  u = rnorm(n, 0, 5)  # u_i
  # length(weight)

  us <- weights <- heights <- genders <- g <-  vector("list", n)

  for (i in 1:n) {
    heights[[i]] <- rnorm(ns[[i]], height[i], 5)
    weights[[i]] <- rnorm(ns[[i]], -20 + 0.8*heights[[i]] + gender[i]*10+ u[i], 5)  # e_ij

    g[[i]] <- rep(i, each=ns[i]) 
    genders[[i]] <- rep(gender[i], each=ns[i])
    us[[i]] <- rep(u[i], each=ns[i])
  }

  heights <- unlist(heights)
  g <- factor(unlist(g))
  genders <- factor(unlist(genders))
  weights <- unlist(weights)
  us <- unlist(us)

  dat <- data.frame(weights, heights, genders, g, us)

  library(nlme)
  lmeMod <- lme(weights ~ genders + heights, random=~1|g, data= dat)
  lmeMod2 <- lme(weights ~ heights, random = ~1|g, data= dat)
  lmeMod3 <- lme(weights ~ genders, random = ~1|g, data= dat)

  contrasts(dat$g) <- contr.treatment(nlevels(g))
  lmMod <- lm(weights ~ heights + g, data= dat)
  lmMod2 <- lm(weights ~ genders + g, data= dat)

  res[iexp, ] = c(coef(lmeMod)[1,"heights"],
                  coef(lmeMod2)[1,"heights"],
                  coef(lmMod)["heights"])

  res2[iexp, ] = c(coef(lmeMod)[1,"genders1"],
                   coef(lmeMod3)[1,"genders1"],
                   coef(lmMod2)["genders1"])
}

#dfRes <- as.data.frame(res)
apply(res, 2, function(x) { paste0(round(mean(x),02),"(", round(sd(x),02),")") })

##    random_full random_reduced          fixed 
##    "0.8(0.06)"   "0.88(0.06)"    "0.8(0.08)"

library(ggplot2)
#library(tidyr)
dfRes <- data.frame(value=c(res), cond = rep(colnames(res), each=nrow(res)))
ggplot(dfRes, aes(x=value, col=cond, fill=cond)) + 
  geom_density(alpha=0.2) + 
  geom_vline(xintercept=0.8, linetype='dotted') +
  scale_x_continuous(name='estimated coefficient of `height`')

plot of chunk unnamed-chunk-7

위의 시뮬레이션 결과를 보면 독립변수와 개체별 효과에 상관이 있을 때, RE 모형을 쓰면 키의 고정효과를 과대 추정하게 됨을 확인할 수 있다.

#dfRes2 <- as.data.frame(res2)
apply(res2, 2, function(x) { paste0(round(mean(x),02),"(", round(sd(x),02),")") })

##    random_full random_reduced          fixed 
##      "10(1.7)"     "18(2.83)"    "17.83(14)"

library(ggplot2)
#library(tidyr)
dfRes2 <- data.frame(value=c(res2), cond = rep(colnames(res2), each=nrow(res2)))
ggplot(dfRes2, aes(x=value, col=cond, fill=cond)) + 
  geom_density(alpha=0.2) + 
  geom_vline(xintercept=10, linetype='dotted') +
  scale_x_continuous(name='estimated coefficient of `gender`')

plot of chunk unnamed-chunk-8

하지만 FE를 쓴다고 언제나 비편향적인 것은 아니다. 위의 결과를 보면 gender 계수의 경우는 FE를 써도 추정량은 편향이 있다. 이는 물론 gender와 오차항 e_{ij}의 상관(내생성)에 의한 것이다. (위의 그래프를 보면 위의 상황에서 RE가 아니라 반드시 FE를 써야 한다는 주장에 고개를 약간 갸우뚱할 수도 있을 것이다. RE이 비해 FE가 저렇게나 분산이 큰데?)

위의 그래프에서 각 모형은 다음과 같다.

RE(Random effects) full 모형( \(\textrm{weight}_{ij} = \beta_0 + \beta_{1} \textrm{gender}_i + \beta_2 \textrm{height}_{ij} + u_{i} + e_{ij}\ \ (u_i \sim \mathcal{N}(0, \sigma_u^2))\) )
RE(Random effects) reduced 모형( \(\beta_0 + \beta_2 \textrm{gender}_{i} + u_i’ + e_{ij}\ \ (u_i’ \sim \mathcal{N}(0, \sigma_u^2))\) )
FE(Fixed effects) 모형( \(\beta_0 + \beta_2 \textrm{gender}_{i} + u_i’ + e_{ij}\) )

다시 통계학의 고정 효과와 임의 효과

사실 수식으로 고정효과와 임의효과를 써보면 이 둘의 차이가 모호하다. 다음의 수식에서 \(\vec{\beta}\) 는 고정 효과, \(\vec{u}\) 는 임의 효과를 나타낸다.

\[\vec{y} = \mathbb{X} \vec{\beta} + \mathbb{Z} \vec{u} + \vec{\epsilon}\]

그런데 다음처럼 행렬 \(\mathbb{X}\) 와 \(\mathbb{Z}\) 를 합치고, 행벡터 \(\vec{\beta}\) 와 \(\vec{u}\) 를 합쳐서 쓸 수도 있다.

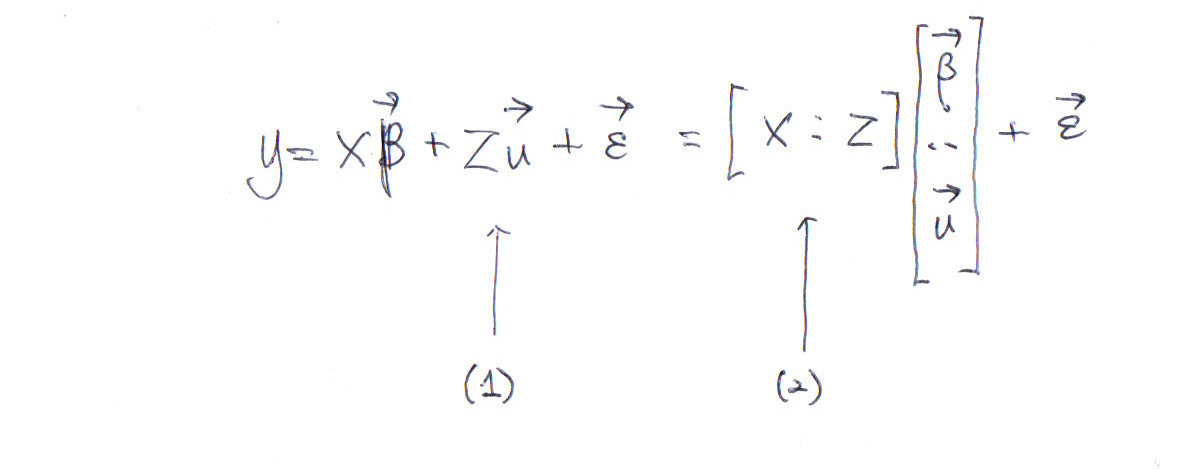
구체적인 예로 다음과 같은 경우를 들 수 있다.

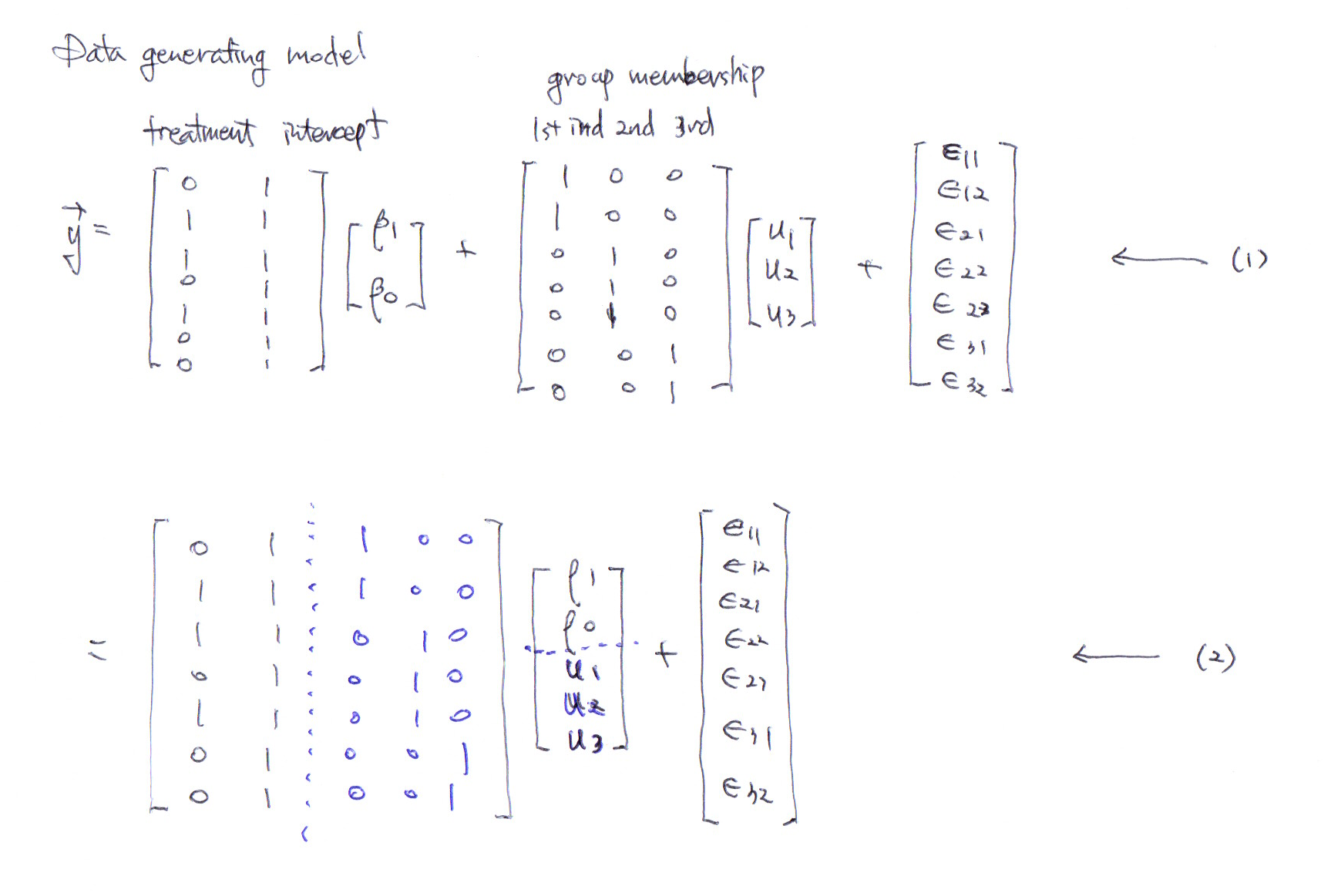
그렇다면 고정효과와 임의효과의 차이는 무엇인가?

이 둘의 차이는 고정 효과에 대해서는 특별한 가정이 들어가지 않지만 임의 효과 \(\vec{u} = (u_1, u_2, \cdots, u_g)^T\) 에 대해서는 분포 가정 \(u_i \sim \mathcal{N}(0, \sigma_u^2)\) 을 하고, \(u_i\) 를 각각 추정하지 않고, 대신 단 하나의 모수 \(\sigma_u^2\) 를 추정한다는 차이가 있다.

만약 \(u_i\) 를 계량 경제학에서 말하는 고정효과 모형으로 추정한다면 위의 모형에서 “분포 가정 \(u_i \sim \mathcal{N}(0, \sigma_u^2)\) "를 제거해 주기만 하면 된다.

따라서 고정효과와 임의효과의 차이는 효과(여기서는 \(\vec{\beta}\) 또는 \(\vec{u}\) 로 나타나는 계수)를 어떤 모형 또는 어떤 가정을 통해 추정하느냐의 차이만 있을 뿐이다.

계량 경제학에서 고정효과와 임의효과의 구분이 필요한 이유는 내생성에서 살펴본 것처럼 인과 관계 추정을 위해서는 정확한 모형을 사용해야 하기 때문이다.

개체별 효과가 설명변수와 상관이 있음에도 불구하고, 개체별 효과가 설명변수와 독립이라는 가정을 가지고 있는 임의 효과 모형을 쓴다면 설명변수의 인과 관계 계수 추정량이 편향(bias)을 가지게 된다.

하지만 인과관계를 추정하지 않는다면 임의효과 모형도 괜찮다. 예측 모형으로는 개체별 효과가 설명변수와 상관이 있어도 큰 문제가 없다.

오히려 더 중요한 문제는 과연 임의 효과가 가정한 것처럼 정규분포를 따른다고 할 수 있는지가 될 것이다. 하지만 몇몇 연구들은 임의 효과가 정말 정규분포를 따르지 않는다고 해도 큰 문제가 없다고 보고하였다(참고자료 3).

실험 자료를 분석하는 경우에 개체별 효과가 정말 정규분포와 유사하다면 random effects model을 쓰지 않을 이유가 없어 보인다. 실험 조건을 fixed effect로 두고, group을 random effects로 사용한다면, 평균적으로 fixed effect와 random effects에 상관이 없다. (물론 group의 갯수가 작을 경우에는 우연히 생길 수도 있으므로 fixed effects model를 사용해야 할 것이다.) 그리고 다른 통제 변수의 경우는 그 변수의 계수를 인과 관계로 해석하지 않는 이상 괜찮을 것 같다.

어쨋든 정리

어쩃든 정리를 해보자면, 전통적인(?) 통계학에서 fixed effect와 random effect의 차이는 계수의 분포에 대한 가정이 있으냐 없느냐의 차이이다. 그리고 추정을 할 때 fixed effect는 모수를 명시적으로 추정하고, random effect의 경우는 분포에 대한 모수(예. 분산)을 추정한다는 차이가 있다.

계량 경제학에서 임의 효과는 임의효과 모형(RE model)으로 추정해도 인과관계를 비편향적으로 추정할 수 있는 효과이고, 고정 효과는 임의효과 모형으로 추정하면 편향이 생기기 때문에 고정효과 모형을 사용하여 추정해야 인과관계 계수를 비편향적으로 추정할 수 있는 효과이다. (계수를 비편향적으로 추정한다. = 계수 추정량이 비편향적이다.) 다시 말해 임의 효과는 설명변수와 독립인 경우이고, 고정 효과는 설명변수와 독립이 아닌 경우이다.

결국 베이지안의 관점에서 볼 때, 임의효과는 사전 분포가 주어진 것으고, 고정효과는 사전분포가 uniform한 경우로 생각할 수 있지 않을까?

다음의 글은 계량생물학(biometrics) 또는 생물통계학(biostatistics) 관점을 다루고 있다. (솔직히 자세히 읽어보진 않았지만, 집단들이 모집단 전체를 나타내느냐 그렇지 않느냐의 구분은 중요해 보인다.)

참고 자료

부록: JAGS를 활용한 베이지안 분석과 `lme` 또는 `lm`을 활용한 임의효과/고정효과 모형의 비교

Data generation

  n =50;
  ns = sample(3:5, n, replace = TRUE) # length(ns)
  gender = sample(0:1, n, replace = TRUE) # length(gender)
  height = rnorm(n, 160, 10) + gender*10 # length(height)
  u = rnorm(n, 0, 5)  # u_i
  # length(weight)

  us <- weights <- heights <- genders <- g <-  vector("list", n)

  for (i in 1:n) {
    heights[[i]] <- rnorm(ns[[i]], height[i], 5)
    weights[[i]] <- rnorm(ns[[i]], -20 + 0.8*heights[[i]] + gender[i]*10+ u[i], 5)  # e_ij

    g[[i]] <- rep(i, each=ns[i]) 
    genders[[i]] <- rep(gender[i], each=ns[i])
    us[[i]] <- rep(u[i], each=ns[i])
  }

  heights <- unlist(heights)
  g <- factor(unlist(g))
  genders <- factor(unlist(genders))
  weights <- unlist(weights)
  us <- unlist(us)

  dat <- data.frame(weights, heights, genders, g, us)

  library(nlme)
  lmeMod <- lme(weights ~ genders + heights, random=~1|g, data= dat)
  lmeMod2 <- lme(weights ~ heights, random = ~1|g, data= dat)
  lmeMod3 <- lme(weights ~ genders, random = ~1|g, data= dat)

임의 효과 모형

JAGS

model <- '

model {
    # model
    for (i in 1:N) {
        #predW[i] <- beta0 + beta1*genders[i] + beta2*heights[i] + groupmean[g[i]]
        predW[i] <- beta0 + beta2*heights[i] + groupmean[g[i]]
        weights[i] ~ dnorm(predW[i], tauE)
    }

    # priors
    for (igroup in 1:G) {
        groupmean[igroup] ~ dnorm(0, tauG)
    }

    tauE <- pow(sigmaE, -2)
    tauG <- pow(sigmaG, -2)

    #beta0 ~ dnorm(0, 0.01)
    #beta1 ~ dnorm(0, 0.01)
    #beta2 ~ dnorm(0, 0.01)
    beta0 ~ dunif(-100,100)
    #beta1 ~ dunif(-100,100)
    beta2 ~ dunif(-1000,1000)
    sigmaE ~ dunif(0,1000)
    sigmaG ~ dunif(0,1000)
}
'
cat(model, file="currentModel.j")

require(rjags)
myj <- jags.model('currentModel.j',
                  data = list('weights' = weights-mean(weights), 
                              'heights' = heights-mean(heights),
                              'genders'= genders,
                              'N' = length(weights),
                              'G' = nlevels(g),
                              'g' = as.numeric(as.character(g))),
                  n.chains = 3)

# set n.iter here ex. n.iter =5000
update(myj, n.iter = n.iter)
n.thin=1
mcmcsamp <- 
  coda.samples(myj, 
               c('beta0', 'beta1', 'beta2', 'sigmaE', 'sigmaG'), 
               n.iter*n.thin, thin=n.thin)

summary(mcmcsamp)

## 
## Iterations = 6001:11000
## Thinning interval = 1 
## Number of chains = 3 
## Sample size per chain = 5000 
## 
## 1. Empirical mean and standard deviation for each variable,
##    plus standard error of the mean:
## 
##            Mean      SD  Naive SE Time-series SE
## beta0  0.001029 0.91480 0.0074693       0.029572
## beta2  0.827124 0.05655 0.0004618       0.001270
## sigmaE 4.826100 0.28072 0.0022921       0.003521
## sigmaG 5.927431 0.73537 0.0060043       0.010025
## 
## 2. Quantiles for each variable:
## 
##           2.5%     25%       50%    75%  97.5%
## beta0  -1.7909 -0.5963 0.0000117 0.5947 1.8332
## beta2   0.7162  0.7896 0.8265548 0.8653 0.9395
## sigmaE  4.3096  4.6331 4.8124548 5.0065 5.4091
## sigmaG  4.6327  5.4101 5.8738156 6.3918 7.5322

plot(mcmcsamp)

plot of chunk unnamed-chunk-12

print(mean(weights))

## [1] 119.3505

lme

lmeMod <- lme(weights ~ genders + heights, random=~1|g, data= dat)
lmeMod2 <- lme(weights ~ heights, random=~1|g, data= dat)
#summary(lmeMod)
intervals(lmeMod2)

## Approximate 95% confidence intervals
## 
##  Fixed effects:
##                   lower        est.      upper
## (Intercept) -37.4291885 -19.2095342 -0.9898798
## heights       0.7230944   0.8318989  0.9407034
## attr(,"label")
## [1] "Fixed effects:"
## 
##  Random Effects:
##   Level: g 
##                    lower     est.    upper
## sd((Intercept)) 4.559427 5.777233 7.320309
## 
##  Within-group standard error:
##    lower     est.    upper 
## 4.272828 4.783595 5.355418

고정효과 모형

JAGS

model <- '

model {
    # model
    for (i in 1:N) {
        #predW[i] <- beta0 + beta1*genders[i] + beta2*heights[i] + groupmean[g[i]]
        predW[i] <- beta0 + beta2*heights[i] + groupmean[g[i]]
        weights[i] ~ dnorm(predW[i], tauE)
    }

    # priors
    groupmean[1] ~ dnorm(0, 100000)I(-0.005,0.005) # dummy coding
    for (igroup in 2:G) {
        #groupmean[igroup] ~ dnorm(0, tauG)
        groupmean[igroup] ~ dunif(-100,100)
    }

    tauE <- pow(sigmaE, -2)
    tauG <- pow(sigmaG, -2)

    #beta0 ~ dnorm(0, 0.01)
    #beta1 ~ dnorm(0, 0.01)
    #beta2 ~ dnorm(0, 0.01)
    beta0 ~ dunif(-100,100)
    #beta1 ~ dunif(-100,100)
    beta2 ~ dunif(-1000,1000)
    sigmaE ~ dunif(0,1000)
    sigmaG ~ dunif(0,1000)
}
'
cat(model, file="currentModel.j")

require(rjags)
myj <- jags.model('currentModel.j',
                  data = list('weights' = weights-mean(weights), 
                              'heights' = heights-mean(heights),
                              'genders'= genders,
                              'N' = length(weights),
                              'G' = nlevels(g),
                              'g' = as.numeric(as.character(g))),
                  n.chains = 3)

update(myj, n.iter = n.iter)

n.thin=1
mcmcsamp <- 
  coda.samples(myj, 
               c('beta0', 'beta2', 'sigmaE', 'sigmaG'), 
               n.iter*n.thin, thin=n.thin)

summary(mcmcsamp)

## 
## Iterations = 6001:11000
## Thinning interval = 1 
## Number of chains = 3 
## Sample size per chain = 5000 
## 
## 1. Empirical mean and standard deviation for each variable,
##    plus standard error of the mean:
## 
##            Mean        SD  Naive SE Time-series SE
## beta0   -1.0553   2.14677 0.0175283       0.192093
## beta2    0.7781   0.07624 0.0006225       0.002680
## sigmaE   4.8235   0.27971 0.0022838       0.003784
## sigmaG 495.8028 287.72874 2.3492953       2.376685
## 
## 2. Quantiles for each variable:
## 
##           2.5%     25%      50%      75%    97.5%
## beta0  -5.0352  -2.561  -1.0240   0.4047   3.2214
## beta2   0.6291   0.726   0.7777   0.8303   0.9281
## sigmaE  4.3193   4.631   4.8078   5.0003   5.4234
## sigmaG 23.9875 245.228 492.5443 744.7671 973.1308

plot(mcmcsamp)

plot of chunk unnamed-chunk-16

print(mean(weights))

## [1] 119.3505

lm

lmMod <- lm(weights ~ heights + g, data= dat)
confint(lmMod, "heights")

##             2.5 %    97.5 %
## heights 0.6290757 0.9264142

Tags: 계량경제학 계량생물학 고정효과 반복측정 선형모형 임의효과 종단면 패널 혼합효과

admin

Comments on this post

3 Comments

EconStat

2021년 1월 17일

위에 예시중에 계량 모형 FE추정에서

FE(Fixed effects) 모형( β0+β2genderi+u′i+eij )

이부분의 편향이 크게 나온 것이 u’i가 height 를 포함하는 오차인데 그것이

개체별 특성을 나타내지 못하기 때문인 것 같네요

즉, u’i 는 i만의 개별오차인데 height는 ij 로 보통 패널 데이터에서 j는 시간 t일탠데 이러면 개별오차가 되질 않아서 그런 것 같습니다.

응답

EconStat

2021년 1월 17일

더 나아가서 heightij 가 오차(ui가 아니라 uij식으로)로 들어가면 gender와 내생성을 일으켜 FE추정으로 편향이 생길수밖에 없군요

응답

admin

2021년 1월 22일

네 맞습니다. 내생성 문제입니다.

응답

2024 11월
일	월	화	수	목	금	토
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30