심슨과 버크슨

심슨의 역설(Simpson's paradox)

R의 datasets::UCBAdmissions은 1973년 UC Berkeley의 대학원 입학 시험 결과를 보여 준다.

1973년 UC 버클리(Berkeley) 대학은 성차별로 고소를 당한다. 지원자 중 남성은 44%가 합격했지만, 여성은 35%만이 합격을 했기 때문이다. 다음은 버클리 대학원 입학 결과를 그래프로 보여주고 있다.

# from help(UCBAdmissions)
require(graphics)
## Data aggregated over departments
apply(UCBAdmissions, c(1, 2), sum)

##           Gender
## Admit      Male Female
##   Admitted 1198    557
##   Rejected 1493   1278

library(vcd)
mosaic(apply(UCBAdmissions, c(1,2), sum), shade=TRUE, legend=TRUE)

#mosaicplot(apply(UCBAdmissions, c(1, 2), sum),

만약 학과별로 자료를 보면 다음과 같다.

round(prop.table(ftable(Admit ~ Dept + Gender, UCBAdmissions), margin=1), 2)

##             Admit Admitted Rejected
## Dept Gender                        
## A    Male             0.62     0.38
##      Female           0.82     0.18
## B    Male             0.63     0.37
##      Female           0.68     0.32
## C    Male             0.37     0.63
##      Female           0.34     0.66
## D    Male             0.33     0.67
##      Female           0.35     0.65
## E    Male             0.28     0.72
##      Female           0.24     0.76
## F    Male             0.06     0.94
##      Female           0.07     0.93

for (idim in 1:dim(UCBAdmissions)[3]) {
  mosaic(UCBAdmissions[,,idim], shade=TRUE, legend=TRUE, main=dimnames(UCBAdmissions)[[3]][idim])  
}

전체 지원자를 보면 남성의 합격률이 여성의 합격률보다 높다. 하지만 학과별로 나눠 보면 A 학과의 경우 여성의 합격률이 높고, 나머지 학과는 거의 비슷하다. 어떻게 이런 일이 일어날 수 있는가?

결론부터 말하자면, 성은 학과 선택에 영향을 미치고 다시 학과에 의해 합격률이 영향을 받는다. 그리고 여성은 남성에 비해 합격률이 낮은 학과에 대한 지원율이 높았다.

사실 여러 번 얘기해도 이해하기 어려운 개념이다. 다시 한번 설명해보자.

각 학과별로 살펴보면, 성별에 따른 합격률의 차이가 없었다. 하지만 여성의 경우 합격률이 낮은 학과(인문대, 사회대의 경우 정원에 비해 지원자가 많아 합격률이 낮다)에 대한 지원이 많아고, 남성의 경우 합격률이 높은 학과(자연대, 공대 등)에 대한 지원이 많다. 따라서 학과별로 성에 따른 합격률이 없었지만, 여성의 경우 합격률이 낮은 학과에 대한 지원이 많아서 전체 여성에 대한 합격률을 계산해보면 남성에 비해 낮았던 것이다.

이는 다음과 같이 그래프로 그려볼 수도 있다. 학과를 생각하지 않고 남/녀와 합격률만 본다면 다음과 같은 인과관계 모형을 그려 볼 수 있다.

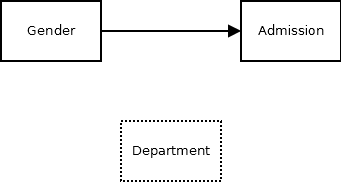
하지만 이는 학과를 고려하지 않았기 때문이며, 학과를 모형에 추가하여 실제 인과관계 모형을 그려보면 다음과 같다. 학과는 합격율에 영향을 주고, 성별이 학과 선택에 영향을 주지면, 성별이 합격율에 영향을 주지는 않는다.

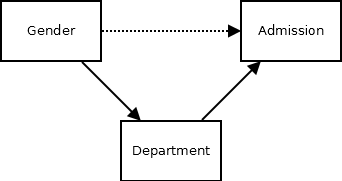
이는 내생성에서도 살펴봤듯이 통제변수를 적절히 포함하지 않아서 오차와 설명변수에 상관이 생겼기 때문이다. (참 인과관계 모형에서 \(합격률 = f(0 \cdot 남녀 + e)\) 라고 할 때, 남자일 때 \(e\) 는 양수이고, 여자일 때 \(e\) 는 음수이다.)

다음은 R의 glm으로 분석한 결과이다. 통제변수로 무엇을 포함시키느냐에 따라 GenderFemale의 계수가 달라짐을 확인해보자.

require(tidyr)
UCBAdf <- as.data.frame(UCBAdmissions)
df <- spread(UCBAdf, key='Admit', value='Freq')
summary(glm(cbind(Admitted, Rejected) ~ Gender, family=binomial, data=df))

## 
## Call:
## glm(formula = cbind(Admitted, Rejected) ~ Gender, family = binomial, 
##     data = df)
## 
## Deviance Residuals: 
##      Min        1Q    Median        3Q       Max  
## -16.7915   -4.7613   -0.4365    5.1025   11.2022  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -0.22013    0.03879  -5.675 1.38e-08 ***
## GenderFemale -0.61035    0.06389  -9.553  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 877.06  on 11  degrees of freedom
## Residual deviance: 783.61  on 10  degrees of freedom
## AIC: 856.55
## 
## Number of Fisher Scoring iterations: 4

summary(glm(cbind(Admitted, Rejected) ~ Gender + Dept, family=binomial, data=df))

## 
## Call:
## glm(formula = cbind(Admitted, Rejected) ~ Gender + Dept, family = binomial, 
##     data = df)
## 
## Deviance Residuals: 
##       1        2        3        4        5        6        7        8  
## -1.2487  -0.0560   1.2533   0.0826   1.2205  -0.2076   3.7189   0.2706  
##       9       10       11       12  
## -0.9243  -0.0858  -0.8509   0.2052  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept)   0.58205    0.06899   8.436   <2e-16 ***
## GenderFemale  0.09987    0.08085   1.235    0.217    
## DeptB        -0.04340    0.10984  -0.395    0.693    
## DeptC        -1.26260    0.10663 -11.841   <2e-16 ***
## DeptD        -1.29461    0.10582 -12.234   <2e-16 ***
## DeptE        -1.73931    0.12611 -13.792   <2e-16 ***
## DeptF        -3.30648    0.16998 -19.452   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 877.056  on 11  degrees of freedom
## Residual deviance:  20.204  on  5  degrees of freedom
## AIC: 103.14
## 
## Number of Fisher Scoring iterations: 4

#summary(glm(cbind(Admitted, Rejected) ~ Gender * Dept, family=binomial, data=df))

이때 다음과 같이 오해하기 쉽다.

그렇다면 인과 관계를 추정하기 위해서는 될 수 있으면 많은 통제 변수를 포함하여 모형을 구성하면 되는거 아닌가?

음.. 딱히 그렇지 않다. 다음의 예를 보자.

버크슨의 역설(Berkson's paradox)

심슨의 역설에 익숙한 사람도 버크슨의 역설은 생소할 수 있다. 버크슨의 역설은 통제 변수와 인과관계 추정에서 심슨 역설의 정반대 지점에 놓여있다.

심슨 역설은 통제 변수를 포함하지 않아 생기는 가짜 인과 관계를 보여준다면, 버크슨의 역설은 통제 변수를 포함해서 생기는 가짜 인과관계를 보여준다.

다음의 예를 보자.

식당의 평점 = 맛 + 인테리어

식당의 평점은 크게 두 가지 요소(맛과 인테리어)에 대한 평점의 합으로 이루어진다. 따라서 인과관계 모형은 다음과 같다.

\[평점 = 맛 + 인테리어 + e\]

이를 그래프로 표현하면 다음과 같다.

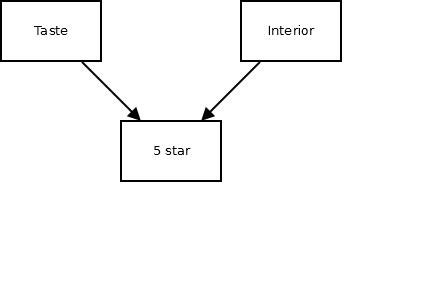
이때 맛과 인테리어는 서로 인과 관계가 없기 때문에 다음과 같이 인과관계 계수는 유의미하지 않다.

N <- 1000
taste <- rnorm(N)
interior <- rnorm(N)
score <- taste + interior + (e=rnorm(N))
dat <- data.frame(taste, interior, score)
summary(lm(taste ~ interior, data=dat))

## 
## Call:
## lm(formula = taste ~ interior, data = dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.58375 -0.66466  0.00948  0.66956  2.45230 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.02091    0.03014  -0.694    0.488
## interior    -0.01450    0.03093  -0.469    0.639
## 
## Residual standard error: 0.9525 on 998 degrees of freedom
## Multiple R-squared:  0.0002203,  Adjusted R-squared:  -0.0007815 
## F-statistic: 0.2199 on 1 and 998 DF,  p-value: 0.6392

하지만 score(평점)을 통제변수를 넣어 회귀 분석을 하면, 다음과 같이 interior(인테리어)는 taste(맛)을 감소시키는 것으로 나타난다.

summary(lm(taste ~ interior + score, data=dat))

## 
## Call:
## lm(formula = taste ~ interior + score, data = dat)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -2.0488 -0.4223 -0.0136  0.4515  2.2760 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -0.02000    0.02147  -0.932    0.352    
## interior    -0.46642    0.02637 -17.687   <2e-16 ***
## score        0.47923    0.01538  31.162   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6783 on 997 degrees of freedom
## Multiple R-squared:  0.4935, Adjusted R-squared:  0.4925 
## F-statistic: 485.8 on 2 and 997 DF,  p-value: < 2.2e-16

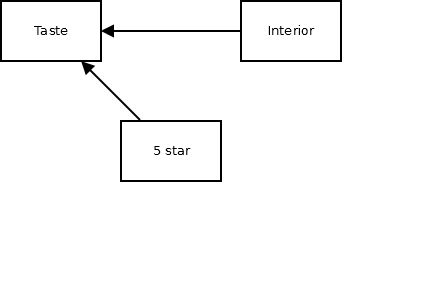
이에 대한 간단한 설명은 다음과 같다. 평점이 같은 경우, 인테리어가 높다면, 맛은 낮아지게 마련이다. 이는 예측모형으로는 훌륭하다. 평점이 인테리어와 맛 점수의 합이기 때문에 중간 평점의 식당은 (중 인테리어, 중 맛), (고 인테리어, 저 맛), (저 인테리어, 고 맛) 중의 하나일 것이다. 이런 상황(평점을 통제한 상태)에서 인테리어가 낮을 수록 맛이 좋다고 기대할 수 있다.

여친 : “자기야, 이 식당은 평점은 엄청 높은데 인테리어는 별로네. 다른 식당 갈까?”

이글을 읽은 남친 : “버크슨의 역설이라고 있어. 여긴 아마 맛이 끝내줄꺼야!”

매개 효과 모형

이런 문제는 매개 효과 모형에서도 마찬가지이다. 매개변수만을 넣어 회귀분석을 하면 매개 변수의 인과관계 계수를 과대 또는 과소 추정하게 되고, 독립변수에 매개변수를 통제변수로 놓어 회귀분석을 하면 총효과가 아니라 직접효과(총효과-간접효과)만을 추정하게 된다.

이런 연유로 많은 경제학 논문들이 여러 변수를 통제변수로 넣어서 분석해보기도 하고, 빼놓고 해보기도 하면서 가정에 따라 결론이 어떻게 달라지는 살펴본다. 하지만 개인적으로 그렇게 통제 변수를 선택하는 것만으로 인과 관계를 정확하게 추정할 수 있을지는 의문이다. 일단 통제 변수로 포함시키고 안 하고는 이론적 배경에 의해 달라져야 하는데 그런 것은 별로 없고, 통제되어야 하지만 통제되지 못한(혹은 관찰되지 못한) 변수가 있다면 결론은 다시 바뀔 수 있으며, 통제변수와 결과 변수의 관계가 선형적이라는 보장도 없으며…

결론

통제 변수를 많이 넣는다고 좋은 것은 아니다.

예측 모형이라면 과적합이 일어나지 않는 한도에서 설명 변수를 많이 넣어서 나쁠 것은 없지만,

인과관계 모형이라면 통제 변수에 따라 결과가 바뀔 수도 있다.