PRML(Pattern Recognition and Machine Learning)이란 책이 있다. Christopher M. Bishop이 쓴 이 책은 ML의 바이블이라고 일컫는다. 대학원에 있을 때에도 누군가 질문을 할 때에면,

“그거 PRML에 있어!"라고 대답하기도 했다는…

하지마 나는 그다지 좋아하지 않았다. 지금 봐도 '정리는 잘 했네'라는 평가를 내릴 순 있다. 하지만 초심자에게 좋은 접근 방법이냐? 이해하기 쉽냐?라고 물었을 때는 주저할 수 밖에 없다.[^1]

[^1]: 사실 이런 문제는 많은 교양 수학책에서도 발견할 수 있다. 정리는 잘 했네. 근데 초심자가 이걸 읽고 이해할 수 있겠어?

라그랑쥐 승수법

이 책의 부록 E에 Lagrange Mulipliers가 나온다. 우리말로는 라그랑쥐 승수법. 발음할 때에는 프랑스 사람인 라그랑쥐를 존중한다는 의미에서 쥐를 약간 '프랑스식'으로 발음해야 한다.

부록 E의 내용이 틀린 내용은 없지만, '이해하기 쉽냐?' 그건 다소 회의적이다.

들어가기

라그랑쥐 승수법은 어떤 제약하의 최적화를 다룬다.

예를 들어, \(g(\vec{x})=0\) 일 때, \(f(\vec{x})\) 를 최대 또는 최소화하는 것이다. ( \(f(\vec{x})\) 를 구하거나, \(f(\vec{x})\) 를 최대/최소화하는 \(\vec{x}\) 를 구한다.)

함수 \(f(\vec{x})\) 또는 \(g(\vec{x})\) 의 구체적인 예를 생각해보자.

\(f(\vec{x}) = x_1^2+x_2^2\) ( \(\vec{x} = (x_1, x_2)\) )라고 할때, \(f(\vec{x})\) 의 최소값은 \(0\) 이고, \(\vec{x}=(x_1, x_2)=(0,0)\) 에서 최소값을 얻을 수 있다.

하지만 \(x_1 + x_1 x_2 + 1= 0\) 이라는 제약 조건을 준다면, \(\vec{x}=(0,0)\) 은 해가 될 수 없다. 왜냐하면 \(x_1=0, x_2=0\) 에서 \(x_1 + x_1 x_2 + 1=0\) 을 만족하지 않기 때문이다.

다시 말해, 질문은 \(x_1 + x_1 x_2 + 1=0\) 일때, \(x_1^2+x_2^2\) 을 최소/최대화하거나, 최소/최대화하는 \((x_1, x_2)\) 을 구하는 것이다.

이 구체적인 상황에 대해 한 번 살펴보고, 다시 일반적인 함수 \(f\), \(g\) 에 대해 얘기해보자.

minimize \(f(x_1, x_2) = x_1^2+x_2^2\)

먼저 제약 조건 없이 \(f(x_1, x_2) = x_1^2+x_2^2\) 을 최소화하는 \(\vec{x}=(x_1, x_2)\) 를 구하는 법을 생각해보자. 가장 손쉬운 방법은 \(\nabla f = 0\) 을 만족하는 \((x_1, x_2)\) 를 구하는 것이다.

여기서 \(\nabla f = (\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2})\) 이므로 \(f(x_1, x_2) = x_1^2+x_2^2\) 에 대해 \(\nabla f = (\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2})=(2x_1, 2x_2)\) 이므로 \((2x_1, 2x_2) = (0,0)\) 을 만족하기 위해서는 \((x_1, x_2) = (0,0)\) 이어야 한다.

\(x_1=0, x_2=0\) 일 때, \(f(x_1, x_2)\) 는 \(0\) 을 최소값으로 갖는다.

minimize \(f(x_1, x_2) = x_1^2+x_2^2\) s.t. \(x_1 + x_1x_2 + 1=0\)

보통 $x_1 + x_1x_2+ 1=0$을 만족하면서 \(f(x_1, x_2) = x_1^2+x_2^2\) 의 최소값을 구하는 것을 다음과 같이 표기하기도 한다.

minimize \(f(x_1, x_2) = x_1^2+x_2^2\) s.t. \(x_1 + x_1x_2 + 1=0\)

여기서 s.t.는 such that의 약자이다.

어쨋든, \(f(x_1, x_2)\) 의 최대값 또는 그 때의 \((x_1, x_2)\) 는 어떻게 구할 수 있을까?

다음의 논리를 따라가 보자.

만약 \(x_1+x_1x_2+1=0\) 이라는 제약 조건이 없다면 \(f(\vec{x})\) 의 최대/최소는 \(\nabla f = \vec{0}\) 에서 얻어진다. (여기서 \(\vec{0}\) 은 입력 변수의 갯수 길이의 \(0\) 벡터이다.)

하지만 \(\nabla f=(2x_1, 2x_2) = (0,0)\) 에서 \(x_1+x_1x_2+1=0\) 이 만족되지 않는다. \((x_1, x_2)=(0,0)\) 에서 \(x_1+x_1x_2+1\) 을 구해 보면 \(0+0+1=1\) 이 된다.

그렇다면 반대로 \(x_1+x_1x_2+1=0\) 일 때 $\nabla f$는 어떤 값을 가지게 될까?

혹은 \(x_1+x_1x_2+1=0\) 을 만족하면서 \(f(\vec{x})\) 를 최대화하려면 \(\nabla f\) 는 어떤 조건을 만족시켜야 하는가?

\(\nabla f(\vec{x})=\vec{0}\)

다시 제약조건이 없을 때, \(\nabla f(\vec{x})=\vec{0}\) 의 조건을 생각해보자. 이 조건을 만족시키는 점 \(\vec{x}\) 에서 \(f\) 가 최대 혹은 최소인 것은 다음의 식에 유추 가능하다.

\[ f(\vec{x} + \vec{\epsilon}) \approx f(\vec{x}) + \nabla f(\vec{x}) \cdot \vec{\epsilon}\]

\(\nabla f(\vec{x})\) 는 점 \(\vec{x}\) 에서 \(f(\vec{x})\) 의 국소적인 함수값을 일차함수로 근사한 것이라 생각할 수 있다. 만약 \(f(\vec{x})\) 가 주위의 모든 값보다 크다면 \(f(\vec{x})\) 는 최소/최대값이 될 가능성이 있다.

만약 \(\vec{\epsilon}\) 의 크기가 매우 작다면, \(\vec{\epsilon}\) 의 방향에 상관 없이, 위의 식이 성립한다. 여기서 \(\nabla f(\vec{x})\) 은 \(\vec{x}\) 와 같은 차원의 벡터이다. 만약 \(\nabla f(\vec{x})\) 이 \(\vec{0}\) 이 아니라고 생각해보자. \(\nabla f(\vec{x}) \cdot \vec{\epsilon}\) 이 양수라면, \(\nabla f(\vec{x}) \cdot (-\vec{\epsilon})\) 는 음수이므로, \(f(\vec{x})\) 은 최소값이나 최대값이 될 수 없다. (왜냐하면 \(f(\vec{x}+\vec{\epsilon})\) 은 \(f(\vec{x})\) 보다 크거나, 작기 때문이다.)

따라서 \(f(\vec{x} + \vec{\epsilon}) \approx f(\vec{x}) + \nabla f(\vec{x}) \cdot \vec{\epsilon}\) 에서 모든 방향의 \(\epsilon\) 에 대해 \(f(\vec{x}) = f(\vec{x}+\vec{\epsilon}) = f(\vec{x}) + \nabla f(\vec{x}) \cdot \vec{\epsilon}\) 이 성립하기 위해서는 \(\nabla f(\vec{x})=0\) 이어야 한다.[^2]

[^2]: 고등학교에서 \(ax=0\) 이 어떤 \(x\) 에 대해서도 성립하려면 \(a=0\) 이어야 한다고 배우지 않았는가?

( 국소적으로 \(f(\vec{x})\) 가 변하지 않는다는 국소적으로 \(f(\vec{x})\) 가 상수 함수임을 나타낸다. 그렇기 때문에 이 값이 과연 최대값인지, 최소값인지, 혹은 \(\vec{x}\) 가 saddle-point인지 확인할 수 없다. 다시 말해 \(\nabla f(\vec{x}) =0\) 은 \(f(\vec{x})\) 가 최대 혹은 최소값이기 위한 필요조건이다.)

\(g(\vec{x})=0\)

이제 \(g(\vec{x})=0\) 을 생각해보자. 함수 \(g\) 에 대해서도 다음과 같이 쓸 수 있다.

\[ g(\vec{x} + \vec{\epsilon}) \approx g(\vec{x}) + \nabla g(\vec{x}) \cdot \vec{\epsilon}\]

그리고 \(g(\vec{x})=0\) 을 만족하는 \(\vec{x}\) 은 전체 입력 공간에서 극히 일부분임을 기억하자.

예를 들어 제약식 \(x_1+x_1x_2 + 1=0\) 에서 \((x_1, x_2)=(-1,0)\) 은 제약식을 만족한다. 하지만 \(\vec{\epsilon}=(0.1, 0.1)\) 로 했을 때 \(\vec{x}+\vec{\epsilon}=(-1+0.1, 0+0.1)=(-0.9, 0.1)\) 은 \(x_1+x_1x_2+1=0\) 을 만족하지 않는다.

만약 어떤 점 \(\vec{x_a}\) 가 \(g(\vec{x_a})=0\) 을 만족할 때, \(g(\vec{x_a}+\vec{\epsilon})=0\) 가 되는 것은 쉽지 않은 일이다. 그렇다면 \(g(\vec{x_a}+\vec{\epsilon})=0\) 가 되려면 \(\vec{\epsilon}\) 은 어떤 조건을 만족해야 하는가?

\(g(\vec{x_a}+ \vec{\epsilon}) = g(\vec{x_a})\) 가 되려면 \(\nabla g(\vec{x_a}) \cdot \vec{\epsilon}\) 가 \(0\) 이 되면 된다. 위의 식을 확인하자.

그리고 \(\nabla g(\vec{x}) \cdot \vec{\epsilon}=0\) 은 두 벡터 \(\nabla g(\vec{x})\) 과 \(\vec{\epsilon}\) 의 사잇각이 90도임을 나타낸다.

이 결과를 적용해보자. \(g(\vec{x})=0\) 을 만족하면서 \(f(\vec{x})\) 를 최대화하려고 할 때, 더이상 \(\vec{\epsilon}\) 은 모든 방향을 고려할 필요가 없다. \(g(\vec{x})=0\) 이고, 매우 작은 \(\vec{\epsilon}\) 에 대해 \(g(\vec{x}+\vec{\epsilon})=0\) 이 성립하려면, \(\nabla g(\vec{x}) \cdot \vec{\epsilon} = 0\) 을 만족해야 하므로, \(f(\vec{x})\) 를 최대화할 때에도 \(\nabla g(\vec{x}) \cdot \vec{\epsilon} = 0\) 을 만족하는 \(\vec{\epsilon}\) 만을 고려하면 된다.

\(f(\vec{x} + \vec{\epsilon}) \approx f(\vec{x}) + \nabla f(\vec{x}) \cdot \vec{\epsilon}\) s.t. \(g(\vec{x}) = 0\)

자, 다시 \(f(\vec{x} + \vec{\epsilon}) \approx f(\vec{x}) + \nabla f(\vec{x}) \cdot \vec{\epsilon}\) 을 보자. 이번에는 무제약(어떤 \(\vec{\epsilon}\) 도 가능)이 아니라, \(g(\vec{x})=0\) 을 만족하는 제약에서 살펴보자.

다시 말해, \(\nabla g(\vec{x}) \cdot \vec{\epsilon} = 0\) 을 만족하는 모든 \(\vec{\epsilon}\) 에 대해 \(\nabla f(\vec{x}) \vec{\epsilon}=0\) 을 만족시키려면 어떤 조건이 필요한가?

제약 하의 최적화: 그래디언트의 관점

\(\nabla g(\vec{x}) \cdot \vec{\epsilon} = 0\) 을 만족하는 모든 \(\vec{\epsilon}\) 에 대해 \(\nabla f(\vec{x}) \cdot \vec{\epsilon}=0\) 을 만족시키려면 어떤 조건이 필요한가?

이 조건은 \(g(\vec{x})=0\) 을 만족하고, \(f(\vec{x})\) 를 최대/최소화는 점 \(\vec{x_{\textrm{optim}}}\) 의 조건을 그래디언트로 표현한 것이라고 할 수 있다.

\(g(\vec{x})=0\) 을 만족하는 점 \(\vec{x}\) 와 그 주변의 점 \(\vec{x}+\vec{\epsilon}\) 을 생각해보자. 국소적으로( \(\vec{\epsilon}\) 의 크기가 매우 작을 때), \(\nabla g(\vec{x}) \cdot \vec{\epsilon} = 0\) 을 만족해야 한다.

\(f(\vec{x})\) 가 최대/최소점이라면 \(\vec{x}\) 는 국소적으로 \(\nabla f(\vec{x}) \cdot \vec{\epsilon} = 0\) 을 만족한다.

자 그렇다면 \(\nabla g(\vec{x}) \vec{\epsilon} = 0\) 을 만족하는 모든 \(\vec{\epsilon}\) 에 대해 \(\nabla f(\vec{x}) \vec{\epsilon}=0\) 을 만족시키려면 어떤 조건이 필요한가?

구체적인 예

다시 구체적인 예로 돌아가보자.

\(1+ x_1 + x_1 x_2 = 0\) 일 때, \(x_1^2 + x_2^2\) 를 최소화해보자.

우선 \(f(x_1, x_2)\) 의 전역 최소화점 \((0,0)\) 이 \(1+ x_1 + x_1 x_2 = 0\) 를 만족하는지 확인한다. 만족하지 않는다.

다음으로 \(\nabla g(x_1, x_2) \cdot \vec{\epsilon} = 0\) 을 만족하는 \(\vec{\epsilon}\) 에 대해 \(\nabla f(x_1, x_2) \cdot \vec{\epsilon} =0\) 을 만족하려면?

구체적으로 \(\nabla f(1,2) = (2,4)\) 이다. 무제약하에서도 최대/최소는 아니다. \(\nabla g \cdot \vec{\epsilon} = (3,1)\cdot \vec{\epsilon}=0\) 을 만족하는 모든 \(\vec{\epsilon}\) 에 대해 \(\nabla f(x_1, x_2) \cdot \vec{\epsilon} = (2, 4)\cdot \vec{\epsilon} = 0\) 을 만족하는가?

예를 들어 \(\vec{\epsilon}=(2,-1)\) 일 때, \(\nabla g(1,2)\cdot (2,-1)=6-1=5\) 로 \((1,2)\) 에서 \((2,-1)\) 로 이동할 경우 \(g(\vec{x})\) 의 값이 변하게 된다는 것을 알 수 있다.

\(x_1, x_2\) 를 미지수로 두고 풀어보면, \((1+x_2,x_1)\cdot(\epsilon_1, \epsilon_2) = (1+x_2)\epsilon_1 + x_1 \epsilon_2 = 0\) 에서 \(\epsilon_1=-\frac{x_1}{1+x_2}\epsilon_2\) 임을 알 수 있다. 모든 \(\epsilon_2\) 에 대해 \(\nabla f(x_1,x_2)\cdot (\epsilon_1, \epsilon_2)=0\) 이 되려면 \(x_1, x_2\) 는 어떤 값이 되어야 할까? \(\nabla f(x_1, x_2)\cdot (\epsilon_1, \epsilon_2) = (2x_1,2x_2)\cdot(-\frac{x_1}{1+x_2}\epsilon_2, \epsilon_2)=-(\frac{2x_1^2}{1+x_2} + 2x_2)\epsilon_2 = 0\) 인 모든 \(\epsilon_2\) 에 대해 성립하려면, \((-\frac{2x_1^2}{1+x_2} + 2x_2)\) 가 \(0\) 이 되어야 한다.

그리고 \(g(\vec{x}) = 0\) 이므로 \(1+x_1 + x_1x_2=0\) 이다.

따라서 다음의 두 등식을 모두 만족하는 \(x_1, x_2\) 가 제약하의 \(f(\vec{x})\) 을 최대/최소화하는 후보가 된다.

\(-\frac{x_1^2}{1+x_2} + 2x_2 = 0\)

\(1+x_1+x_1x_2=0\)

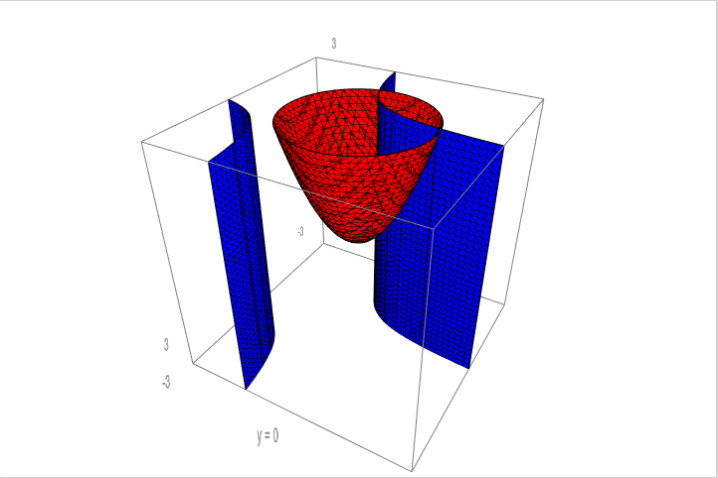
(위의 그래프는 https://cocalc.com 에서 다음의 코드로 작성되었다.

p1 = implicit_plot3d(x+x*y + 1 == 0, (x,-3,3), (y,-3,3), (z,-3,3), texture='blue', mesh=True)
p2 = implicit_plot3d(x^2+y^2 == z, (x,-3,3), (y,-3,3), (z,-3,3), texture='red', mesh=True)
p1 + p2

)

간단하게

두 조건을 다시 써보자.

\(\nabla g(\vec{x})\cdot \vec{\epsilon}=0\)

\(\nabla f(\vec{x})\cdot \vec{\epsilon}=0\)

첫 번째 식에서 두 번째 식을 빼면, \(\nabla g(\vec{x})\cdot \vec{\epsilon} – \nabla f(\vec{x})\cdot \vec{\epsilon}=0\) 이고, \(\left( \nabla g(\vec{x}) – \nabla f(\vec{x}) \right)\cdot \vec{\epsilon} =0\) 을 얻을 수 있다.

만약 모든 \(\vec{\epsilon}\) 에 대해 \(\left(\nabla g(\vec{x}) – \nabla f(\vec{x}) \right)\cdot \vec{\epsilon} =0\) 이 성립하길 원한다면, \(\nabla g(\vec{x}) = \nabla f(\vec{x})\) 이 성립해야 한다.

하지만 잠깐!

위에서 모든 방향에 대해 고려할 필요가 없다고 했잖아?

라그랑쥐 승수법을 암기하는 우리의 자세

"거의 모든 수학은 암기해서 적절히 적용하면 그만이다"란 주류 철학계의 주장을 받아들인다면,

\(g(\vec{x})=0\) 을 만족하면서, \(f(\vec{x})\) 을 최대 혹은 최소화하려면,

\(\nabla f(\vec{x}) – \lambda g(\vec{x}) = 0\) 과 \(g(\vec{x})=0\) 을 만족하는 \(\vec{x}\) 을 구하면 된다.

위의 예를 보자. \(f(\vec{x}) = x_1^2 + x_2^2\) 이고 \(\nabla(f) =(2x_1, 2x_2)\) 이다.
\(g(\vec{x}) = x_1 + x_1x_2 + 1\) 이고, \(\nabla(g) = (1+x_2, x_1)\) 이다.

이제 라르랑쥐 방법에 의해 \(f(\vec{x})\) 을 최대/최소화하는 \(\vec{x}=(x_1, x_2)\) 는 다음을 만족한다.

\[(2x_1, 2x_2) = \lambda (1+x_2, x_1)\]

\[x_1 + x_1 x_2 + 1 = 0\]

\(2x_1 = \lambda( 1+x_2)\) 와 \(2x_2 = \lambda x_1\) 에서 \(\lambda\) 를 제거하려면 ( \(\lambda \neq 0\) ), 첫 번째 식에서 두 번째 식을 나눈다.

\[\frac{x_1}{x_2} = \frac{1+x_2}{x_1}\]

따라서 다음의 두 식을 모두 만족하는 \((x_1, x_2)\) 구하면 된다.

\(x_1 + x_1x_2 + 1 =0\), \(x_1^2 = (1+x_2)x_2\)

첫 번째 식에서 \(x_1(1+x_2) = -1\) , \(x_1 = \frac{-1}{1+x_2}\) 을 얻고 이 식을 아래 식에 대입하면,

\[\frac{1}{(1+x_2)^2} = (1+x_2)x_2\]

\(1 = (1+x_2)x_2(1+x_2)^2\) 을 잘 풀어보면, \(x_2 \approx -1.8192, 0.38028\) 을 얻을 수 있다.³

이 값을 이용해 \(x_1\) 을 구하고 \(f(x_1, x_2)\) 을 구한 후, 그 값중에서 최대/최소값을 찾을 수 있다.

풀어보니 괜찮은 예가 아니었다는 생각이 든다. (깔끔히 떨어지는 예제를 만드는 것도 쉽지 않은 일이다.)

어쨋든 이 방법이 수치적이 방법보다 나은 점은 정확한 해(수치적으로 푼 근사해가 아니라)를 얻을 수 있다는 점, 그리고 함수 \(f\) 또는 \(g\) 에 문자 \(a\) , \(b\) , \(c\) 등이 포함되어 있어도 풀 수 있다는 점이 있다!

라그랑쥐 승수법을 이해하는 우리의 자세

다음의 조건을 보자.

\(\nabla g(\vec{x})\cdot \vec{\epsilon}=0\)

이때 \(\lambda_1\neq 0\) 이라면, \(\lambda_1(\nabla g(\vec{x})\cdot \vec{\epsilon})=0\) 과 위의 식은 동치이다.

\(\nabla f(\vec{x})\cdot \vec{\epsilon}=0\) 에 대해서도 동일한 얘기를 할 수 있지만 생략하자.

이제 \(\nabla g(\vec{x})\cdot \vec{\epsilon}=0\) 을 만족하는 \(\vec{\epsilon}\) 에 대해 \(\nabla f(\vec{x})\cdot \vec{\epsilon}=0\) 을 만족시키는 방법은 없을까?

3차원 공간을 생각해보자. \(\vec{a} \cdot \vec{x} =0\) ( \(\vec{a}\) 상수, \(\vec{x}\) 변수) 는 원점 \(\vec{0}\) 을 지나고 벡터 \(\vec{a}\) 에 수직인 평면을 나타낸다.

이 평면의 모든 점은 \(\lambda \vec{a} \cdot \vec{x}=0\) ( \(\lambda \neq 0\) )의 꼴로 나타낼 수 있다.

따라서 \(f(\vec{x}) = \lambda g(\vec{x})\) 을 만족해야 한다.

이때 \(\lambda \neq 0\) 조건이 최대/최소값을 구하는데에는 중요하지 않음을 유의하자. 왜냐하면 \(\lambda =0\) 일때, \(f(\vec{x})=\vec{0}\) 이고, \(g(\vec{x})=0\) 과 \(f(\vec{x})=0\) 을 만족하면 \(f(\vec{x})\) 도 최대/최소값 후보가 되기 때문이다.

숙제

제약 조건이 두 개 이상일 때와, KKT(Karush-Kuhn_tucker) 조건에 대해 유도하고, 이해하고, 설명해 보세요.