질문: 그래디언트란 무엇인가?[^1]

[^1]: 이 글의 일부는 출간 예정인 <수학의 숨은 원리 2>의 원고 일부를 발췌한 것입니다.

일전에 facebook에서 그래디언트가 무엇인지에 대해 한창 논란이 있었다. 어떤 사람들은 그래디언트가 기울기라고 하고, 어떤 사람은 단순히 방향이라고 했다. 그리곤 다른 사람이 공식 하나를 보여주는 것으로 훈훈히(?) 마무리가 되었다. (그렇지! 수학이란 모름지기 공식으로 말하는 것이다!?)

그런데 정말로, 그래디언트가 무엇인가?

수학은 기호일 뿐이지만, 상상할 수 있다면 쉽다.

사실 수학자들이 엄밀하게 생각하는 수학이란, 아니 적어도 증명을 할때에는, 단순히 기호의 나열이라서 그걸 어떻게 생각해 냈건, 어떻게 상상해 해냈건 상관 없다(주어진 공리와 타당한 연역 규칙을 사용하기만 하면 된다).

예를 들어 1+1=2이고, 이걸 점 2개로 상상하건, 아이스크림 2개로 생각하건 문제가 없다. 사실 점 2개, 아이스크림 2개, 사탕 2개, 막대 2개에서 수 2를 추출해내는 것도 굉장한 추상화, 일반화 과정이 필요하다. 그래서 엄밀하게 말해, 1+1=2와 아이스크림 1개와 아이스크림 1개를 합치면 아이스크림이 2개라는 명제는 a-a=0과 3-3=0만큼이나 큰 간극이 있다(라고 생각하지만,). 계산을 빨리하기 위해 주판을 손가락으로 오르락 내리락한다고 꾸중할 사람도 없다(물론 주판을 사용하는 대부분의 경우는 실제 사물이나 돈을 대상으로 하는 것이겠지만).

대수와 기하

그럼에도 불구하고 데카르트는 기하의 대수화에 성공했으며, 우리는 \(2x+2y=0\) 를 2차원 평면 위의 직선을 나타낸다고 생각할 수 있다. 그리고 대수화된 기하의 중요성은 4차원, 5차원처럼 눈으로 볼 수도 없고, 직관적으로 상상할 수도 없는 대상을 탐구할 때 드러난다.

그래서 그래디언트란 무엇인가?

그래디언트는 1변수 함수 그래프에서 기울기와 비슷한 역할을 하는데, 기울기라고 말하긴 힘들다. 왜냐하면 위에서 얘기한 토론에서도 지적되었듯이 여러 값으로 이루어진 벡터이기 때문이다. 벡터는 흔히 방향과 크기를 동시에 나타낸다고 말한다.

그래서 다른 사람은 그래디언트는 기울기가 아니라 순간변화율이 가장 큰 방향을 나타낸다고 주장했다. 일리가 있는 말이다. 그래디언트 디센트에서도 그래디언트를 쓰는 이유는 함수값을 최대한 빠르게 감소시키기 위해서이다. 함수값을 변화시키려면 입력값을 변화시켜야 하고, 입력값을 어떤 식으로 변화시켜야 함수값을 가장 빠르게 최소화할 수 있는지를 그래디언트가 알려주는 것이다. 하지만 그래디언트라는 벡터 함수는 입력값이 주어졌을 때 벡터를 출력한다. 앞에서 얘기했듯이 벡터는 방향과 크기를 동시에 가지고 있기 때문에 단순히 순간변화율이 가장 큰 방향이라고 하기에는 뭔가 부족하다.

대수학(Algebra)이란?

숫자 2가 돌 2개, 자동차 2개, 바나나 2개의 추상화/일반화라면, 대수학의 변수 \(x\) 는 숫자 \(1,2,3\) 등의 추상화/일반화라고 생각할 수 있다.

대수학에서의 관심은 변수가 포함된 등식, 부등식 등이고, 이들 등식, 부등식은 일정한 조건을 만족하는 모든 구체적인 수에 대해 성립한다. 예를 들어 유명한 산술평균과 기하평균의 관계는 0보다 큰 모든 실수에 대해 성립하고, 그것을 증명할 수 있다!

\[\frac{a+b}{2} \geq \sqrt{ab} \ \ (a \geq 0, b \geq 0)\]

우와! 신기하다. 어떻게 모든 양수에 대해 위의 등식 성립한다는 것을 알았데?

사실 대수학이 기호를 사용하기 때문에 구체적인 수를 사용하던 사람들에게 어렵게 보일 수도 있지만, 그 기호가 무엇을 의미하는지와 상관없이 일정한 공식 또는 방법을 따라 변형을 하면 되기 때문에 대수학의 문제는 컴퓨터도 쉽게 할 수 있는 단순한 작업도 많다.

실제로 대수학에서 사용하는 가장 기본적인 규칙(공리)은 10개를 넘지 않는다.

어쨋든 대수학은 모든 수 또는 특정한 조건을 만족하는 모든 수에서 성립하는 등식, 부등식 등을 밝힌다.

그래디언트를 설명해 달라고?!!!

서론이 길었다. 그래디언트란 다변수 함수의 모든 입력값에서 모든 방향에 대한 순간변화율이다.

그래디언트를 계산하기 위해서는 일단 함수가 필요하다.

우선 1차원 함수에 대한 미분을 생각해보자. 몇몇 사람들은 미분을 단순히 기울기라고 말하는데, 함수를 미분한 결과는 기하학적인 기울기를 계산할 수 있는 함수이다.

예를 들어 \(f(x)=x^2\) 의 미분 함수인 \(f'(x)=2x\) 는 점 0에서 기울기가 0, 점 1에서는 기울기가 \(2\cdot 1= 2\) 임을 알려주고, 이 함수는 모든 점에서의 기울기(순간변화율)을 알려주는 함수이다. (어떻게 변수를 활용하여 모든 입력값에 대해 순간변화율을 알려주는지 음미해보자.)

그래디언트는 주어진 다변수 함수에 대해 벡터 함수가 된다. 특정한 입력값에 대해 벡터를 산출하므로 확실히 순간변화율이라고 말하기엔 어딘가 부족하다.

그래디언트는 정확한 의미는 다음의 식에서 좀 더 살펴볼 수 있다.

\[f(\vec{x}+\vec{\epsilon}) \approx f(\vec{x}) + \nabla f(\vec{x}) \cdot \vec{\epsilon}\]

점 \(\vec{x}\) 에서 매우 작은 \(\vec{\epsilon}\) 에 대해 위의 등식이 성립한다. (왜냐하면 그래디언트를 정의할 때 저게 성립하도록 했기 때문이고 저런 식이 성립하지 않는다면 그래디언트가 존재하지 않는다.)

저 식에 따르면 특정한 방향의 순간변화율을 알고 싶다면 \(\vec{\epsilon}\) 대신에 그 방향의 길이가 1인 벡터를 대입하면 된다. 그리고 어떤 방향에 대해서도 가능하다.

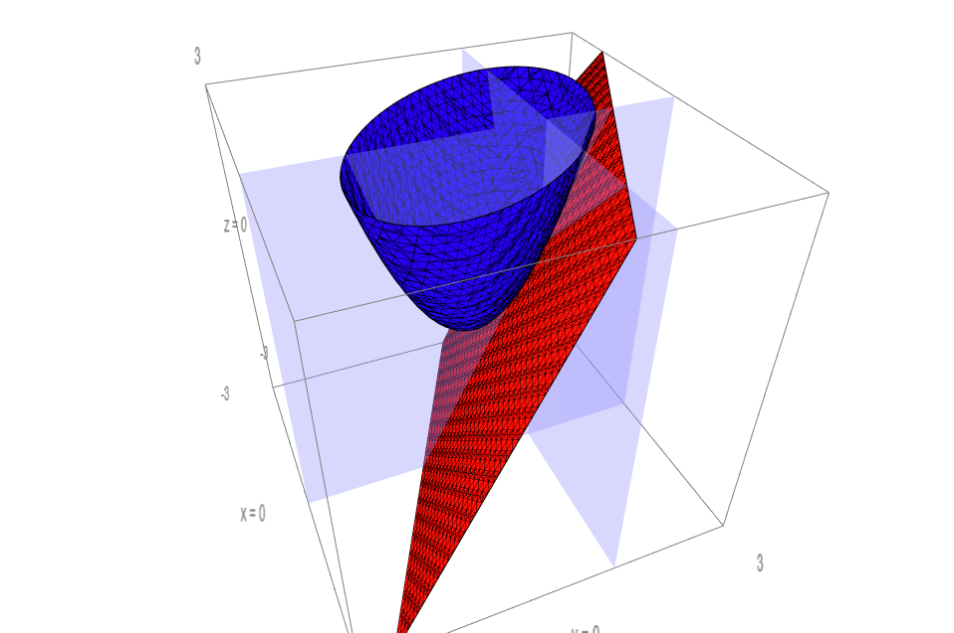
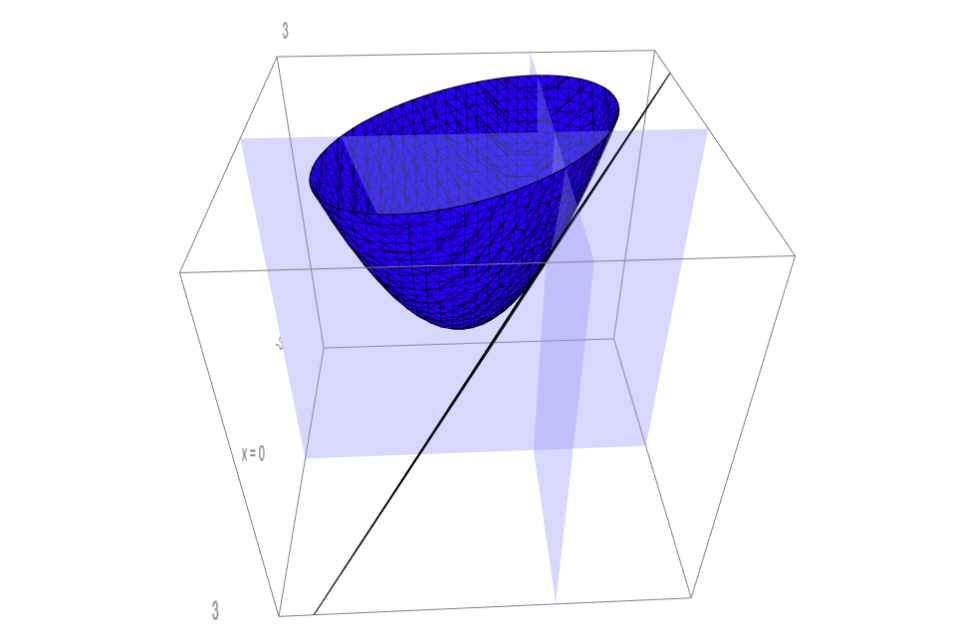
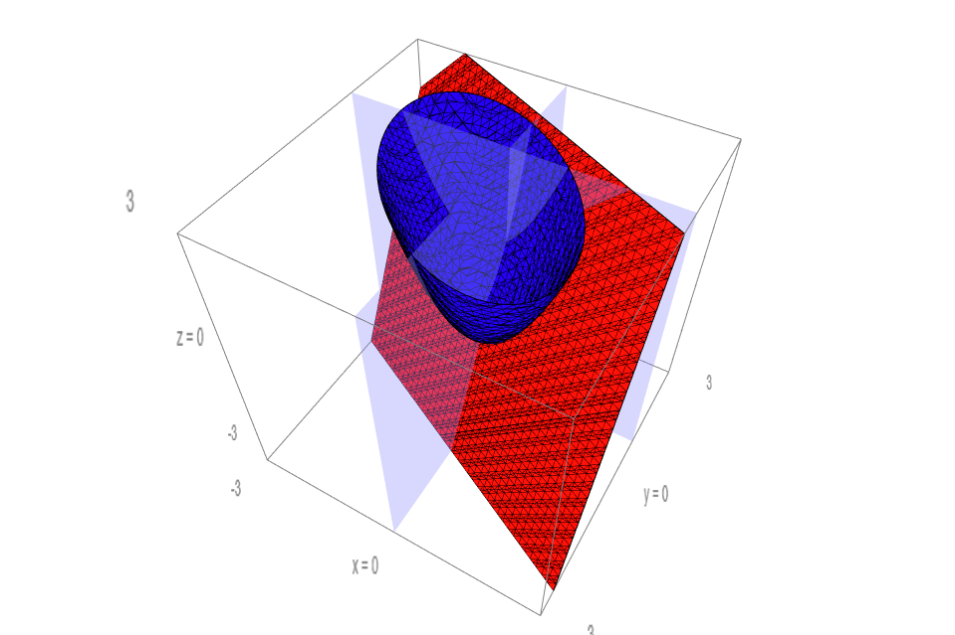
예를 들어보자. \(f(x_1, x_2) = x_1^2 +x_1x_2+ x_2^2\) 에서 \(\nabla{f}=(2x_1+x_2, 2x_2+x_1)^\textrm{T}\) 이고, \((0,1)\) 에서 \(\nabla{f}(0,1)=(1,2)\) 이다. 이때 \((1,1)\) 방향의 순간 변화율을 알고 싶다면, \((1,2)\cdot (1/\sqrt{2},1/\sqrt{2})=3/\sqrt{2}\) 가 된다.

어떤 방향으로의 순간변화율이란 1변수 함수를 생각해보면 쉬울 수 있다.

\((1,1)\) 방향으로 \((x_1, x_2)\) 가 변한다면, \((x_1, x_2) = t(1,1) = (t,t)\) 로 쓸 수 있다. 이는 \((0,0)\) 을 지나가는 경우이고, \((0,1)\) 을 지나가려한다면 \((x_1, x_2) = (t,t)+(0,1)\) 로 쓸 수 있다. 그때 \(f(x_1, x_2) = x_1^2+x_1x_2+x_2^2=t^2+t\cdot(t+1)+(t+1)^2\) 이 된다.

\(f(x_1,x_2)=f(t)=t^2+t(t+1)+(t+1)^2=t^2+t^2+t+t^2+2t+1=3t^2+3t+1\) 이 되고, 이를 미분하면, \(f'(t) = 6t+3\) 이다. 점 \((0,1)\) 은 \(t=0\) 일 때 지나간다. \(f'(0)=3\) .

그런데 \(t\) 가 \(1\) 만큼 움직일 때 \((t,t+1)\) 은 길이 \(\sqrt{2}\) 만큼 움직이므로 이를 보정하면 \(f(t)\) 의 순간변화율(다시 말해 \(f(\vec{x})\) 의 \((1,1)\) 방향 순간변화율)은 \(3/\sqrt{2}\) 가 된다!

# cocalc.com
# Sage Worksheet
var('x y z')
p1 = implicit_plot3d(x^2+x*y+y^2==z, (x,-3,3), (y,-3,3), (z,-3,3), texture='blue', mesh=True)
p2 = implicit_plot3d(x+2*(y-1)==(z-1), (x,-3,3), (y,-3,3), (z,-3,3), texture='red', mesh=True)
p3 = implicit_plot3d(x==0, (x,-3,3), (y,-3,3), (z,-3,3), alpha=0.2)
p4 = implicit_plot3d(y==1, (x,-3,3), (y,-3,3), (z,-3,3), alpha=0.2)
p1 + p2 + p3 + p4

다른 방향으로의 순간변화율도 계산해보자. 그래디언트로 계산해보고, 이변수 함수를 1변수 함수로 만들어서도 계산해 보자.

모든 값에서 모든 방향의 순간변화율을 \(\nabla{f}(\vec{x})\cdot\vec{\epsilon}\) 로 구할 수 있다고?

그렇다! \(|\vec{\epsilon}|=1\) 이고, 그래디언트가 존재한다면, \(\nabla{f}(\vec{x})\cdot\vec{\epsilon}\) 은 모든 점 \(\vec{x}\) 에서 모든 방향 \(\vec{\epsilon}\) 에 대한 순간변화율을 나타낸다. 어떻게 그게 가능하냐고? 그래디언트의 특징이고 변수의 표현력이다!

만약 \(|\vec{\epsilon}|=1\) 을 만족하지 않는다면 \(\nabla{f}(\vec{x})\cdot\vec{\epsilon}\) 는 입력값 \(\vec{x}\) 에서의 순간변화율을 그대로 유지하면서 \(\vec{\epsilon}\) 만큼 입력값을 변화시킬 때의 변화량이라고 말할 수 있겠다.

그리고 이런 맥락에서 \(f\) 의 \(\vec{x}\) 에서 순간변화율을 기준으로 가장 빠르게 \(f\) 를 변화시키는 방향은 \(\frac{\nabla f(\vec{x})}{|\nabla f(\vec{x})|}\) 이고(방향을 나타낼 때에는 보통 길이 1인 벡터를 사용한다), 그때 순간 변화율은 \(\nabla f(\vec{x}) \cdot \frac{\nabla f(\vec{x})}{|\nabla f(\vec{x})|}\) 이 된다. (따라서 \(\nabla f(\vec{x}) \cdot \frac{\nabla f(\vec{x})}{|\nabla f(\vec{x})|}\) 는 입력값 \(\vec{x}\) 에서 함수 \(f\) 의 최대 순간변화율이라고도 할 수 있다.)

여기서 \(\frac{\nabla f(\vec{x})}{|\nabla f(\vec{x})|}\) 은 \(\frac{\vec{a}}{|\vec{a}|}\) 은 벡터 \(\vec{a}\) 와 방향이 같고, 크기는 1인 벡터가 됨을 활용한 것이다.

R에서 그래디언트 구하기

R에서 미분 또는 그래디언트를 구하는 기본적인 함수는 stats::D, stats::deriv가 있다.

?D 또는 ?deriv를 쳐보면, Symbolic and Alorithmic Derivatives of Simple Expressions라고 나온다. 여기서 Simple Expressions는 +, -, *, /, ^, exp, log, sin, cos, tan, sinh, cosh, sqrt, pnorm, dnorm, asin, acos, atan, gamma, lgamma, digamma, trigamma, psigamma(첫 번째 인자에 대해서), log1p, expm1, log2, log10, cospi, sinpi, tanpi, factorial, lfactorial을 포함하는 수식이다.

다음은 D 또는 deriv를 사용하여 간단한 함수의 미분을 구하는 예이다.

expr <- expression(x^2+2*x*y+y^2)
D(expr, name='x')

## 2 * x + 2 * y

deriv(expr, namevec=c('x', 'y'))

## expression({
##     .expr2 <- 2 * x
##     .expr8 <- .expr2 + 2 * y
##     .value <- x^2 + .expr2 * y + y^2
##     .grad <- array(0, c(length(.value), 2L), list(NULL, c("x", 
##         "y")))
##     .grad[, "x"] <- .expr8
##     .grad[, "y"] <- .expr8
##     attr(.value, "gradient") <- .grad
##     .value
## })

expression, quote, 그리고 parse

R에서 expression은 아직 계산되지 않은 수식이라고 생각할 수 있다. 예를 들어 2*x+y를 입력하면 x의 값과 y의 값이 대입되어 2*x+y의 결과가 산출된다.

x=3; y=2
2*x+y

## [1] 8

만약 x와 y에 값이 대입되지 않은 수식을 그대로 저장하고 싶다면, expression 또는 quote를 사용한다.

a <- expression(2*x+y)
print(a)

## expression(2 * x + y)

그리고 이 수식에 따라 실제 계산을 하고 싶다면, eval 함수를 사용한다.

eval(a)

## [1] 8

x=2; y=2;
eval(a)

## [1] 6

D

함수 D는 expression에 대해 한 변수의 편미분을 구한 결과를 expression으로 반환한다.

D(expression(y*cos(x)+x*sin(y)), 'x')

## sin(y) - y * sin(x)

만약 특정 입력값에서의 미분값을 구하고 싶다면, eval( , list(x=, y=))를 사용할 수 있다.

f <- expression(y*cos(x)+x*sin(y))
dfdx <- D(f, 'x')
eval(dfdx, list(x=1, y=pi))

## [1] -2.643559

위의 \(-2.643559\) 는 \(y\cos(x)+x\sin(y)\) 의 \(x\) 편미분 \(\frac{\partial f(x,y)}{\partial x} = \sin(y)-y\sin(x)\) 의 \((x,y)=(1,\pi)\) 에서의 값이다.

\[\frac{\partial f(x,y)}{\partial x}\vert_{(x,y)=(1,\pi)} = \sin(\pi)-\pi\sin(1) \approx -2.643559\]

deriv

deriv 함수도 expression을 받아 expression을 반환하는데, 이 expression은 x와 y가 주어졌을 때, 함수값과 그래디언트를 모두 구해 하나의 변수로 반환한다.

f <- expression(y*cos(x)+x*sin(y))
f2 <- deriv(f, c('x', 'y'))
f2

## expression({
##     .expr1 <- cos(x)
##     .expr3 <- sin(y)
##     .value <- y * .expr1 + x * .expr3
##     .grad <- array(0, c(length(.value), 2L), list(NULL, c("x", 
##         "y")))
##     .grad[, "x"] <- .expr3 - y * sin(x)
##     .grad[, "y"] <- .expr1 + x * cos(y)
##     attr(.value, "gradient") <- .grad
##     .value
## })

이를 활용하는 방법은 다음과 같다.

eval(f2, list(x=1, y=pi))

## [1] 1.69741
## attr(,"gradient")
##              x          y
## [1,] -2.643559 -0.4596977

\(y\cos(x)+x\sin(y)\) 의 \((x,y)=(1,\pi)\) 에서의 값은 \(1.69741\) 이며, 그래디언트는 \((-2.643559, -0.4596977)\) 임을 위의 결과로 알 수 있다.

헤시안까지 구하고자 한다면, deriv3을 사용한다.

f3 <- deriv3(f, c('x', 'y'))
eval(f3, list(x=1, y=pi))

## [1] 1.69741
## attr(,"gradient")
##              x          y
## [1,] -2.643559 -0.4596977
## attr(,"hessian")
## , , x
## 
##             x         y
## [1,] -1.69741 -1.841471
## 
## , , y
## 
##              x             y
## [1,] -1.841471 -1.224606e-16

그 밖에

다음에서 보듯이 expression, quote, parse는 모두 비슷한 역할을 하고 있다.

D(expression(x^2*y), 'x')
D(quote(x^2*y), 'x')
D(parse(text="x^2*y"), 'x')

## 2 * x * y
## 2 * x * y
## 2 * x * y

좀 더 expression과 quote은 다음과 같은 차이가 있다.

expression(x^2+y^2, 2*x*y)

## expression(x^2 + y^2, 2 * x * y)

quote(x^2+y^2, 2*x*y)

## Error in quote(x^2 + y^2, 2 * x * y): 2 arguments passed to 'quote' which requires 1

quote(x^2+y^2)

## x^2 + y^2

a <- expression(x^2+y^2, 2*x*y)
b <- quote(x^2+y^2)
all.equal(a[[1]], b)

## [1] TRUE

R에서 수치 미분

함수 D와 함수 deriv는 앞에서 언급된 함수에 대해서만 미분이 가능하다는 단점이 있다. 수치 미분을 사용하면 그런 제약은 없다. 반면 한 점에 대해서만 계산이 가능하며 D와 deriv처럼 모든 점에서의 기울기를 구하는 함수를 구하지는 못한다.

다음은 함수 \(y\cos(x)+x\sin(y)\) 의 \((1,\pi)\) 에서 그래디언트 값을 구한다.

library(numDeriv)

f<-function(x) {x[2]*cos(x[1])+x[1]*sin(x[2])}

grad(f,c(1, pi))

## [1] -2.6435591 -0.4596977

덤으로 헤시안과 자코비안은 다음과 같다.

hessian(f,c(1,pi))

##           [,1]          [,2]
## [1,] -1.697410 -1.841471e+00
## [2,] -1.841471 -2.082973e-13

g = function(x) { c(x[2]*cos(x[1])+x[1]*sin(x[2]), x[1]^2+x[2]^2)}
jacobian(g, c(1,pi))

##           [,1]       [,2]
## [1,] -2.643559 -0.4596977
## [2,]  2.000000  6.2831853

deriv와 grad 비교

R의 함수 dgamma는 다음의 함수를 나타낸다. (이때 \(k\) = shape, \(\theta\) = scale)

\[f(x; k, \theta) = x^{k-1}\frac{\exp(-x/\theta)}{\theta^k \Gamma(k)}\]

curve(dgamma(x, shape=2, scale=2), xlim=c(0,10))

\((x,k,\theta) = (2, 2, 2)\) 에서 그래디언트를 구하고자 한다.

deriv(expression(dgamma(x,k,th)), c('x', 'k', 'th'))

## Error in deriv.default(expression(dgamma(x, k, th)), c("x", "k", "th")): Function 'dgamma' is not in the derivatives table

deriv로는 dgamma의 미분이 불가능하지만 grad를 통한 수치미분은 가능하다.

f <- function(x) {
  dgamma(x[1], x[2], x[3])
}
grad(f, c(2,2,2))

## [1] -0.2197877  0.1411784 -0.1465251

한 줄 정리

그래디언트란 다변수 함수의 모든 입력값에서 모든 방향으로의 순간변화율이다. 모든 방향의 순간변화율은 함수 \(f(\vec{x})\) 의 어떤 한 점(혹은 모든 점)에서 접하는 접평면의 기울기이다. (접평면의 기울기는 변수 갯수만큼의 숫자가 필요하다.)